Wie wählen wir den besten Typ von Digitalfilter für unsere Anwendung aus? Und was sind die Unterschiede zwischen einem IIR-Filter und einem FIR-Filter?
Advanced Solutions Nederland is blij te kunnen aankondigen dat het ASN Filter Designer Arm MDK5 software pack nu via Keil beschikbaar is om te downloaden! Het filterpakket biedt MDK-gebruikers een eenvoudige manier om het IP van ASN te gebruiken.
Keil MDK is de meest uitgebreide oplossing voor software-ontwikkeling voor Arm-gebaseerde microcontrollers. Voor MDK worden extra softwarecomponenten en ondersteuning voor microcontroller devices geleverd door softwarepakketten. Download hier
UI experience 2020 pack
Na het downloaden van de ASN Filter Designer willen de meeste mensen gewoon met de tool spelen, om een gevoel te krijgen of het voor hen werkt. Maar hoe ga je aan de slag met de ASN Filter Designer? Op basis van goede gebruikersfeedback wordt ASNFD v4.4 nu geleverd met het UI experience 2020-pakket. Dit pakket bevat gedetailleerde coachingstips, een verbeterde gebruikerservaring en stap-voor-stap instructies om je op weg te helpen met je ontwerp.
Een snel overzicht van de ASN Filter Designer v4.4 vindt je hieronder, een geweldige tool voorDSP IIR/FIR digitaal filterdesign!
De ASN Filter Designer heeft een snelle, intuïtieve gebruikersinterface. Ontwerp interactief, valideer en implementeer jouw uw digitale filter binnen enkele minuten in plaats van uren. Het kan echter moeilijk zijn om een eerste begin te maken met DSP-filterontwerp, vooral wanneer je geen diepgaande kennis hebt van digitale signaalverwerking. De meeste mensen willen gewoon experimenteren met een tool om een gevoel te krijgen of het voor hen werkt (ja, natuurlijk zijn er tutorials en video’s). Maar waar begin je dan?
Start onmiddellijk met experimenteren met het filterontwerp
Daarom hebben we het UI Experience 2020-pakket ontwikkeld. Op basis van de feedback van de gebruikers hebben we gedetailleerde tooltips en animaties van de belangrijkste functionaliteiten gemaakt. Binnen enkele minuten krijgt u een kickstart in functionaliteiten zoals chart zoom, panning en design markers.
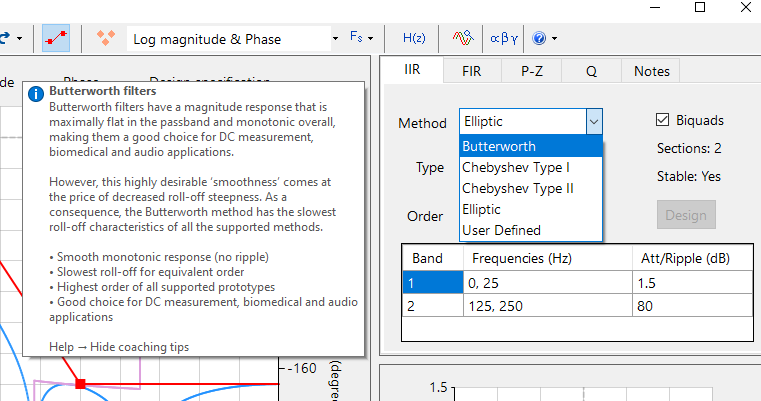
Coachingstips, verbeterde gebruikerservaring, stap-voor-stap instructies
Gebaseerd op de feedback van de gebruiker bevat het UI Experience 2020-pakket:
- Uitgebreide coachingtips
- Gedetailleerde uitleg over ontwerpmethoden en soorten filters
- Verbeterde gebruikerservaring:
- cursors
- animaties
- visuele effecten
- Links naar gedetailleerde werkende oplossingen, tutorials en stap-voor-stap instructies
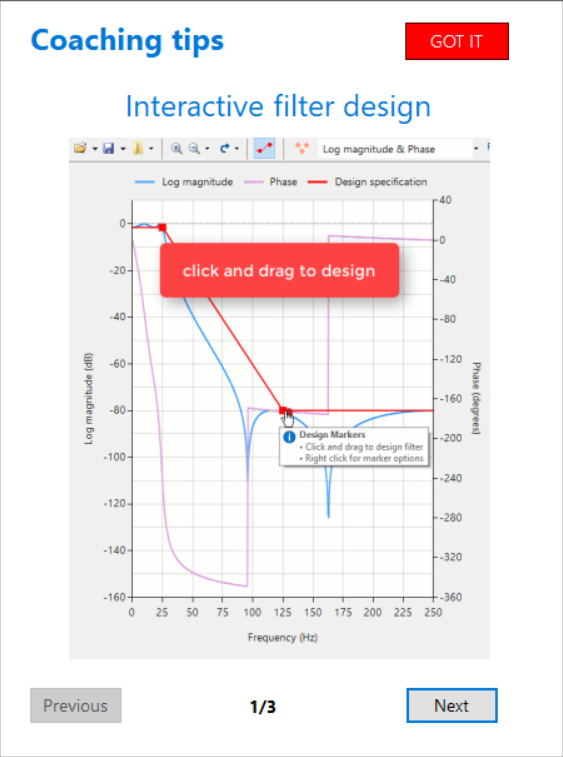
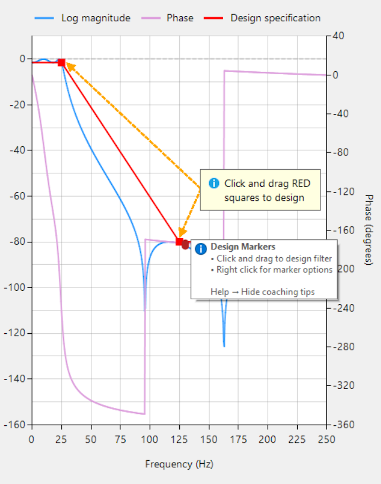
De feedback van de gebruikersgemeenschap is zeer positief! Door het verstrekken van gedetailleerde tooltips en animaties van de belangrijkste functionaliteit, is de eerste stap van het ontwerpen van een filter met jouw gewenste specificaties aanzienlijk vereenvoudigd.
Begin dus meteen met de ASN Filterontwerper en bespaar tot 75% op jouw ontwikkelingskosten!
DSP voor ingenieurs: de ASN Filter Designer is de ideale tool om de sensordata snel te analyseren en te filteren. Maak een algoritme binnen enkele uren in plaats van dagen. Wanneer u met sensorgegevens werkt, herkent u deze uitdagingen waarschijnlijk:
- Mijn sensordatasignalen zijn te zwak om zelfs maar een analyse te maken. Daarom heb ik versterking van de signalen nodig
- Waar ik een vlakke lijn zou verwachten, zien de gegevens eruit als een puinhoop door interferentie en andere vervuiling. Ik moet de gegevens eerst opschonen voordat ik ze analyseer.
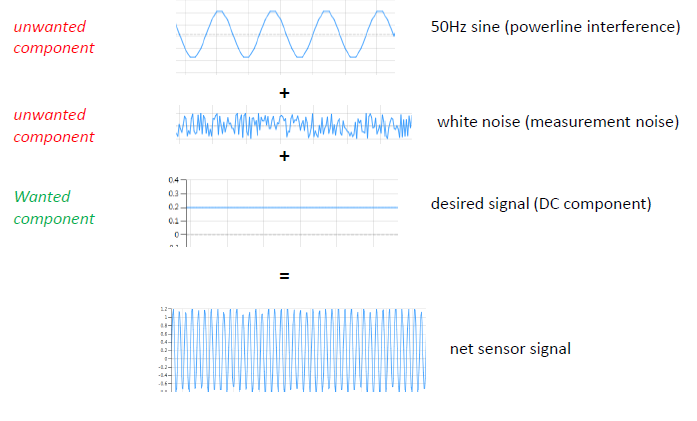
Waarschijnlijk heb je tot nu toe dagen of zelfs weken gewerkt aan signaalanalyse en filtering. Het ontwikkelingstraject is over het algemeen langzaam en zeer pijnlijk. Denk maar eens aan het aantal uren dat je had kunnen besparen als je een ontwerptool had gehad die alle algoritmische details voor jou beheerde. ASN Filter Designer is een standaardoplossing voor de industrie die wordt gebruikt door duizenden professionele ontwikkelaars die wereldwijd aan iot-projecten werken.
Onze nauwe samenwerking met Arm en ST zorgt ervoor dat alle ontworpen filters 100% compatibel zijn met alle Arm Cortex-M processoren, zoals de populaire STM32-familie van ST.
Uitdagingen voor ingenieurs
- 90% van IoT smart sensors zijn gebaseerd op Arm Cortex-M processor technologie
- Sensor signal processing is moeilijk
- Sensoren hebben moeite met interferentie en allerlei ongewenste componenten
- Hoe ontwerp ik een filter dat voldoet aan mijn requirements?
- Hoe kan ik mijn ontworpen filter controleren op testdata?
- Voor betere product performance is schone sensor data nodig
- Tijdrovend proces om een filter op een embedded processor te implementeren
- Tijd is geld!
Ontwerpers verzanden vaak met traditionele tooling. Deze vereist meestal een iteratieve, trial and error aanpak of deskundige kennis. Met deze aanpak gaat kostbare tijd verloren. ASN Filter Designer helpt u met een interactieve ontwerpmethode. Hierbij voert de tool automatisch de technische specificaties in op basis van eisen die de gebruiker grafisch heeft ingevoerd.
Snelle ontwikkeling van het DSP-algoritme
- Volledig gevalideerd filterontwerp: geschikt voor toepassing in DSP, Arm microcontroller, FPGA, ASIC of PC-toepassing
- Automatische gedetailleerde ontwerpdocumentatie: de Filter Designer helpt je met documenatie, waardoor je de peer review kunt versnellen en projectrisico’s verlaagt
- Eenvoudige overdracht: projectdossier, documentatie en testresultaten bieden een gemakkelijk manier voor overdracht aan collega’s of andere teams
- Gemakkelijk in te passen in nieuwe scenario’s: het ontwerp kan eenvoudig worden aangepast aan andere eisen en scenario’s, zoals 60Hz interferentieonderdrukking op de voedingslijn, in plaats van de Europese 50Hz.
ASN Filter Designer: de snelle en intuitieve filter designer
De ASN Filter Designer is het ideale hulpmiddel om sensorgegevens snel te analyseren en filteren. Indien nodig kun je jouw gegevens eenvoudig naar tools als Matlab en Python exporteren voor verdere analyse. Daarom is het ideaal voor ingenieurs die een krachtige tool voor signaalanalyse nodig hebben en een datafilter voor hun IOT-toepassing moeten maken. Zeker als je af en toe een datafilter moet maken. Vergeleken met andere tools creeer je een algoritme binnen enkele uren in plaats van dagen.
Exporteer jouw algoritmes naar Matlab, Python of een Arm microcontroller
Je kunt veel tijd besparen doordat je met ASN Filter Designer algoritmes eenvoudig kunt implementeren in Matlab, Python of direct op een Arm-microcontroller omdat de Filter Designer automatisch code generateert.
Onmiddelijke verlichting
Denk eens aan het aantal uren dat je had kunnen besparen als je een ontwerptool had gehad die alle algoritmische details voor je beheerde.
ASN Filter Designer is een standaardoplossing in de sector die wordt gebruikt door duizenden professionele ontwikkelaars die wereldwijd aan ivd-projecten werken. Onze nauwe samenwerking met Arm en ST zorgt ervoor dat alle filters 100% compatibel zijn met alle Arm Cortex-M processoren.
Hoeveel pijnverzachting kun je voor 145 Euro kopen?
Omdat veel technici onze ASN Filterontwerper voor korte tijd nodig hebben, is een licentie van 145 euro voor slechts 3 maanden mogelijk!
Vraag jezelf maar af: is 145 Euro een eerlijke prijs om te betalen voor onmiddellijke pijnverlichting en resultaat? Wij denken van wel. Bovendien hebben we een licentie voor 1 jaar en zelfs een eeuwigdurende licentie. Download de demo om het zelf te zien of neem contact met ons op voor meer informatie
Hoewel het ontwerp van FIR-filters met lineaire fase een eenvoudige opgave is, geldt dit zeker niet voor IIR-filters die meestal een zeer niet-lineaire faserespons hebben, vooral rond de afsnijfrequenties van het filter. Dit artikel bespreekt waarvoor lineairde eigenschappen die nodig zijn om een digitaal filter een lineaire fase te laten hebben en hoe de passband fase van een IIR filter kan worden aangepast om een lineaire fase te bereiken met behulp van all-pass equalisatie filters.
Waarvoor zijn lineaire fase filters bedoeld?
Digitale filters met lineaire fase hebben het voordeel dat ze alle frequentiecomponenten met dezelfde hoeveelheid vertragen, d.w.z. dat ze de faseverhoudingen van het ingangssignaal behouden. Dit behoud van fase betekent dat het gefilterde signaal de vorm van het oorspronkelijke ingangssignaal behoudt. Deze eigenschap is essentieel voor audiotoepassingen, omdat de signaalvorm van het grootste belang is voor het behoud van de high fidelity in het gefilterde geluid. Nog een ander toepassingsgebied waar dit is vereist, is de ECG biomedische golfvormanalyse, omdat eventuele artefacten die door het filter worden geïntroduceerd, verkeerd kunnen worden geïnterpreteerd als hartafwijkingen.
De volgende grafiek toont de filterprestaties van een Chebyshev type I lowpass IIR op ECG-gegevens – invoergolfvorm (weergegeven in blauw) verschoven door 10 samples (\(\small \Delta=10\)) om de groepsvertraging van het filter ongeveer te compenseren. Merk op dat het gefilterde signaal (in rood weergegeven) de oscillaties rond de ECG-piek heeft verzwakt, verbreed en toegevoegd, wat ongewenst is.
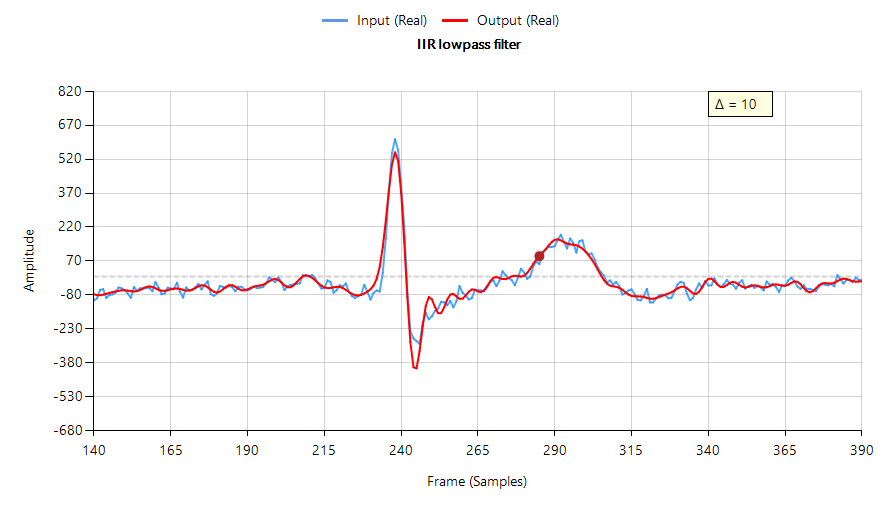
Om een digitaal filter een lineaire fase te laten hebben, moet de impulsrespons van een digitaal filter een conjugaat-even of conjugaat-odd-symmetrie hebben rond het midden van het filter. Dit is gemakkelijk te zien voor een FIR-filter,
Met het volgende constraint op zijn coëfficiënten
welke leidt tot
Naar Eqn. 3 kijkend, zien we dat wortels (nullen) van \(\small H(z)\) ook de nullen moeten zijn van \(\small H^\ast (1/z^\ast)\). Dit betekent dat de wortels van \(\small H(z)\) moet voorkomen in geconjugeerde wederzijdse paren. Bijvoorbeeld wanneer \(\small z_k\) een nul is van \(\small H(z)\), dan moet \(\small H^\ast (1/z^\ast)\) ook een nul zijn.
Waarom hebben IIR filters geen lineaire fase?
Van een digitaal filter wordt gezegd dat het een gebonden ingang, gebonden uitgang stabiel (oftewel: BIBO (Bounded Input, Boundend Output) stabiel), als elke gebonden ingang aanleiding geeft tot een gebonden uitgang. Alle IIR-filters hebben ofwel polen ofwel beide polen en nullen, en moeten BIBO stabiel zijn, d.w.z.
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \tag{4}\)
Hierbij is \(\small h(k)\) de impulsrespons van het filter. Bij het analyseren van Eqn. 4 moet duidelijk zijn dat aan het BIBO-stabiliteitscriterium alleen wordt voldaan als de polen van het systeem binnen de eenheidscirkel liggen, aangezien de eenheidscirkel in het ROC (gebied van convergentie) van het systeem moet worden opgenomen. Het is dus voldoende om te zeggen dat een begrensd ingangssignaal altijd een begrensd uitgangssignaal zal produceren als alle polen binnen de eenheidscirkel liggen.
De nullen daarentegen worden niet beperkt door deze eis en kunnen daardoor overal op het z-vlak liggen, omdat ze niet direct van invloed zijn op de stabiliteit van het systeem. Daarom kan een systeemstabiliteitsanalyse worden uitgevoerd door eerst de wortels van de transferfunctie te berekenen (d.w.z. de wortels van de teller- en noemerpolynomialen) en vervolgens de corresponderende polen en nullen op het z-vlak te plotten.
Door de ontwikkelde logica toe te passen op de polen van een IIR-filter komen we nu tot een zeer belangrijke conclusie waarom IIR-filters geen lineaire fase kunnen hebben..
Een BIBO stabiel filter moet zijn polen binnen de eenheidscirkel hebben, en als zodanig zou een IIR geconjugeerde tegengestelde polen buiten de eenheidscirkel nodig hebben om een lineaire fase te krijgen, waardoor het BIBO onstabiel wordt.
Op basis van deze uitspraak lijkt het niet mogelijk om een IIR te ontwerpen met een lineaire fase. Echter, zoals hieronder besproken, kunnen fase-equalisatiefilters worden gebruikt om de passband-fase respons te lineariseren.
Fase linearisatie met all-pass filters
All-pass fase linearisatiefilters (equalisers) zijn een beproefde methode om de faserespons van een filter te wijzigen zonder de magnitude ervan te beïnvloeden. Een tweede orde (Biquad) all-pass filter wordt gedefinieerd als:
Hierbij is \(\small f_c\) is de centre frequency, \(\small r\) de radius van de polen en \(\small f_s\) de sampling frequency. Merk op hoe de teller- en noemercoëfficiënten als spiegelend aan elkaar zijn gerangschikt. De eigenschap van het spiegelbeeld is wat de all-pass filter zijn gewenste eigenschap geeft, namelijk de ontwerper in staat stellen om de faserespons te veranderen terwijl de magnituderespons constant of vlak blijft over het volledige frequentiespectrum.
Cascadering van een APF (all-pass filter) equalisatie cascade (bestaande uit meerdere APF’s) met een IIR-filter, het basisidee is dat we alleen de fasereactie het passbandgebied moeten lineariseren. De andere gebieden, zoals de overgangsband en de stopband, kunnen worden genegeerd, aangezien eventuele niet-lineairiteiten in deze gebieden van weinig belang zijn voor het totale filterresultaat.
De uitdaging
De APF-cascade klinkt als een ideaal compromis voor deze uitdaging, maar in werkelijkheid is een aanzienlijke hoeveelheid tijd en een zeer zorgvuldige afstemming van de APF-posities nodig om een aanvaardbaar resultaat te bereiken. Elke APF heeft twee variabelen: \(\small f_c\) en \(\small r\) die geoptimaliseerd moeten worden, wat de oplossing bemoeilijkt. Dit wordt verder gecompliceerd door het feit dat hoe meer APF-fasen aan de cascade worden toegevoegd, hoe hoger de totale groepsvertraging (latentie) van het filter wordt. Dit laatste kan problematisch worden voor snelle real-time closed loop controlesystemen die afhankelijk zijn van de lage latency eigenschap van een IIR.
Ondanks deze uitdagingen is de APF-equalizer een goed compromis voor het lineariseren van de kenmerken van een IIR-doorgangsfase.
De APF equaliser
ASN Filter Designer biedt ontwerpers een zeer eenvoudig te gebruiken grafische alle-fase equalizer interface voor het lineariseren van de passband fase van IIR filters. Zoals hieronder te zien is, is de interface zeer intuïtief en stelt het ontwerpers in staat om APF-filters snel te plaatsen en te fine-tunen met de muis. De tool berekent automatisch \(\small f_c\) en \(\small r\), gebaseerd op de markerpositie.
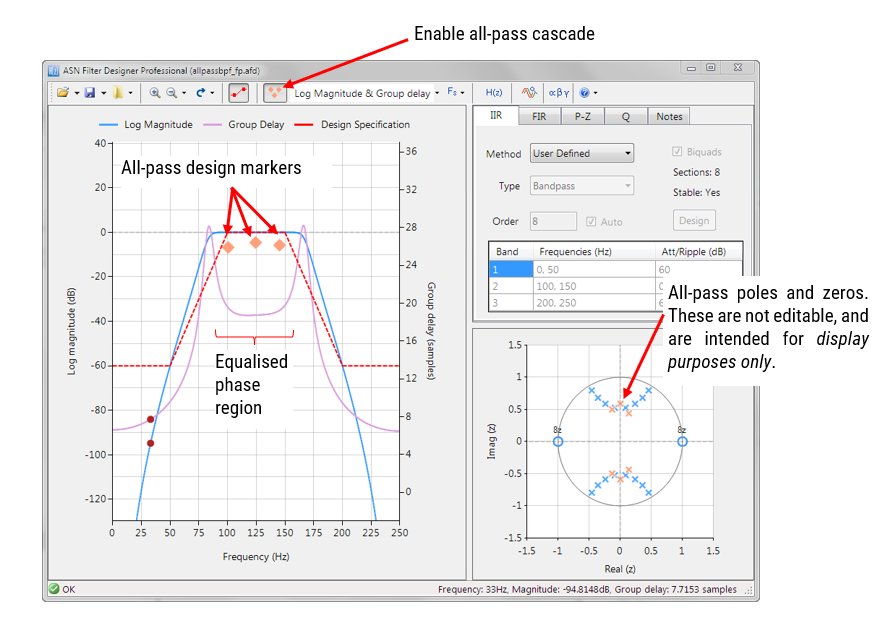
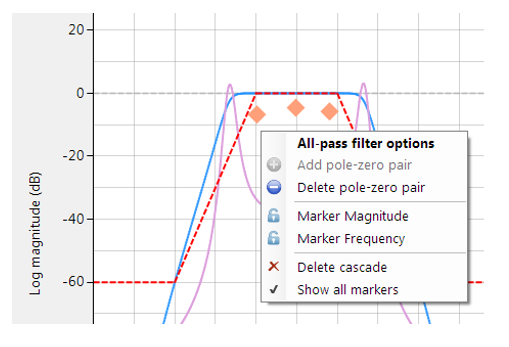
Door met de rechtermuisknop te klikken op de frequentieresponskaart of op een bestaande all-pass design marker wordt een optiemenu weergegeven, zoals links afgebeeld.
U kunt maximaal 10 biquads toevoegen (alleen professionele versie).
Een IIR met lineaire passband fase
Door een equalizer te ontwerpen die bestaat uit drie APF-paren, en deze te cascaderen met het Chebyshev-filter van figuur 1, verkrijgen we een filtergolfvorm die een veel scherpere piek heeft met minder demping en oscillatie dan het oorspronkelijke IIR – zie hieronder. Deze verbetering gaat echter ten koste van drie extra Biquad-filters (de APF-cascade) en een verhoogde groepsvertraging, die nu is opgelopen tot 24 samples ten opzichte van de oorspronkelijke 10 samples.
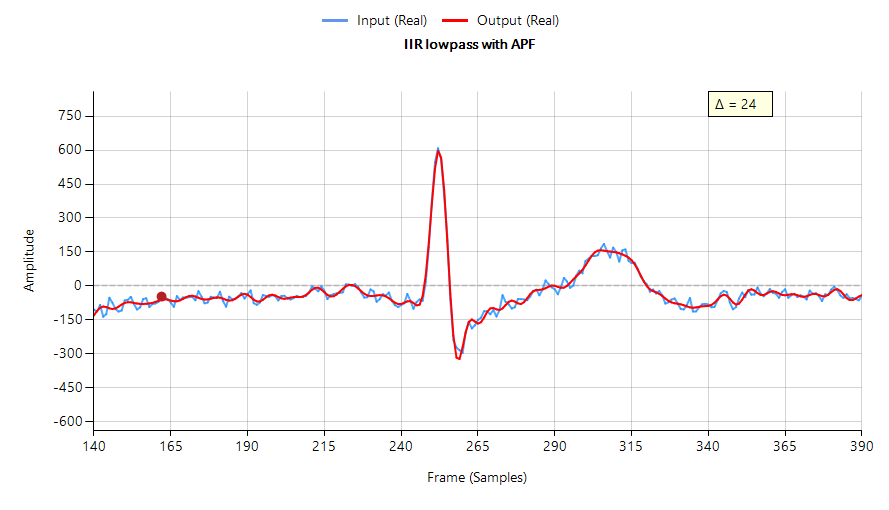
(minimale fasevervorming)
De frequentierespons van zowel het oorspronkelijke IIR als het geequaliseerde IIR worden hieronder weergegeven, waarbij de groepsvertraging (weergegeven in paars) de gemiddelde vertraging van het filter is en een eenvoudiger manier is om de lineariteit te beoordelen.
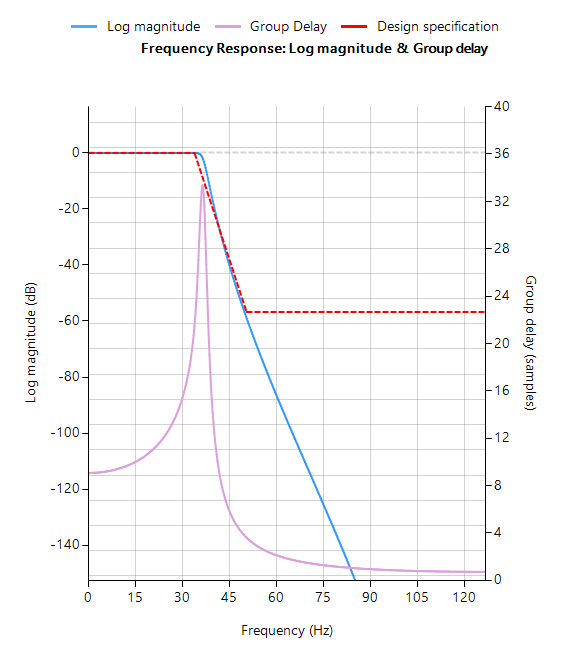
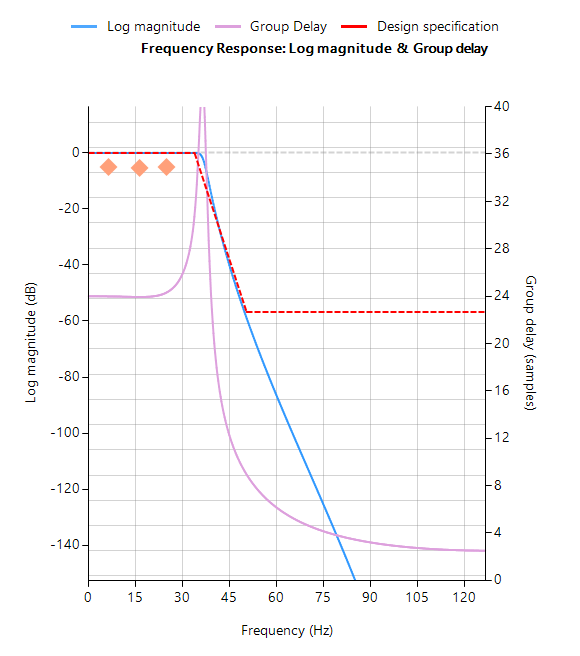
Merk op dat de groepsvertraging van de geëgaliseerde IIR passband (rechts afgebeeld) bijna vlak is, wat bevestigt dat de fase inderdaad lineair is.
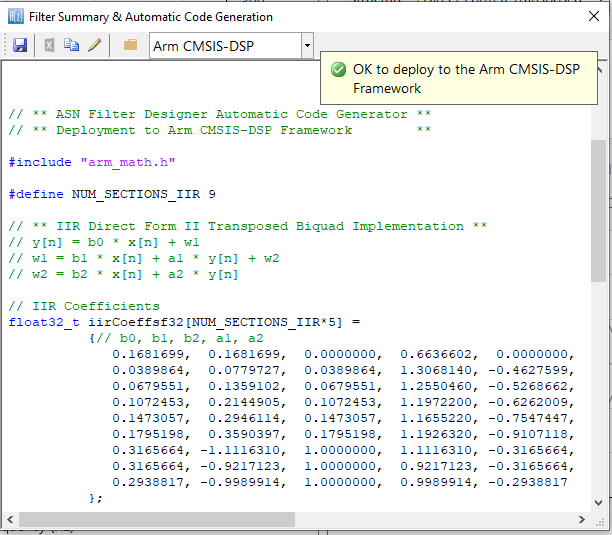
Automatische code generatie naar Arm processor cores via CMSIS-DSP
De automatische codegeneratie-engine van de ASN Filter Designer maakt het mogelijk om een ontworpen filter te exporteren naar Cortex-M Arm-gebaseerde processoren via het CMSIS-DSP software raamwerk. De ingebouwde analyse- en helpfuncties van de tool helpen de ontwerper bij het succesvol configureren van het ontwerp voor implementatie.
Voordat de code wordt gegenereerd, moeten de IIR- en equalisatiefilters (d.w.z. H1- en Heq-filters) eerst opnieuw worden geoptimaliseerd (samengevoegd) tot een H1-filter (hoofdfilter) structuur voor implementatie. Het optiemenu is te vinden onder de P-Z tab in de hoofd UI.
Alle ontwerpen van IIR-filters met floating point moeten gebaseerd zijn op Single Precision arithmetic en ofwel een Direct Form I of Direct Form II getransponeerde filterstructuur. De Direct Form II getransponeerde structuur wordt geadviseerd voor floating point implementatie vanwege de hogere numerieke nauwkeurigheid.
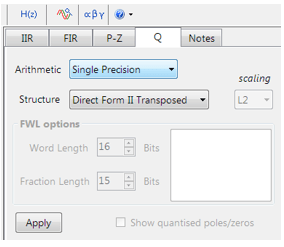
De instellingen voor de kwantiteit en de filterstructuur zijn te vinden onder het tabblad Q (zoals links afgebeeld). Door Arithmetic op Single Precision en Structure op Direct Form II Transposed te zetten en vervolgens op Apply te klikken, wordt de IIR voor het CMSIS-DSP software raamwerk geconficureerd.
Selecteer het Arm CMSIS-DSP raamwerk in het selectievakje in het filteroverzichtsvenster:
De automatisch gegenereerde C-code op basis van het CMSIS-DSP framework voor directe implementatie op een Arm-gebaseerde Cortex-M processor is hieronder weergegeven:
De automatische codegenerator van de ASN Filter Designer genereert alle initialisatiecode, schaling en datastructuren die nodig zijn om het gelineariseerde filter IIR-filter te implementeren via de CMSIS-DSP-bibliotheek van Arm.
Wat hebben we geleerd?
De wortels van een lineaire fase digitaal filter moeten in geconjugeerde wederzijdse paren voorkomen. Hoewel dit geen probleem is voor een FIR-filter, wordt het voor een IIR-filter onhaalbaar, omdat de polen zowel binnen als buiten de eenheidscirkel zouden moeten liggen, waardoor het filter BIBO onstabiel wordt.
De passband fase-respons van een IIR-filter kan worden gelineariseerd met behulp van een APF-equalisatiecascade. De ASN Filter Designer biedt ontwerpers alles wat ze nodig hebben via een zeer eenvoudig te gebruiken, grafische all-pass fase equalizer interface, om met behulp van de muis een geschikte APF-cascade te ontwerpen!
Het gelineariseerde IIR-filter kan worden geëxporteerd via de automatische codegenerator met behulp van de geoptimaliseerde CMSIS-DSP-bibliotheekfuncties van Arm voor gebruik op elke Cortex-M-microcontroller.
Fractional Farrow Delay Filter
Bij signaalverwerking is het soms nodig om de sample frequency van een signaal met een fractie van een sample aan te passen of te verfijnen. Een FIR Farrow vertragingsfilter wordt meestal gebruikt om deze taak te bereiken. Deze kan worden gecombineerd met een traditionele gehele vertragingslijn om een universele fractionele lengte vertragingslijn te bereiken.
Een Fractionele vertraging op basis van een FIR Farrow-structuur kan worden gedefinieerd als:
\(H(z)=(1-\alpha)+\alpha z^{-1}; \; 0 \leq \alpha \leq 1 \)
Welke een fractionele lineaire vertraging oplevert van \(\alpha\) btussen 0 en 1 monster. Een meer universele bouwsteen kan echter worden bereikt door de Farrow-vertragingsstructuur te combineren met een integer vertraging, \(\Delta\)
\(H(z)=(1-\alpha) z^{-\Delta}+\alpha z^{-(\Delta+1)}\)
De onderstaande grafiek toont de magnitude (blauw) en fase (paars) spectra voor \(\Delta=9, \, \alpha=0.52\). Zoals te zien, resulteert het fractionele vertragingselement in een niet-vlak spectrum bij hogere frequenties.
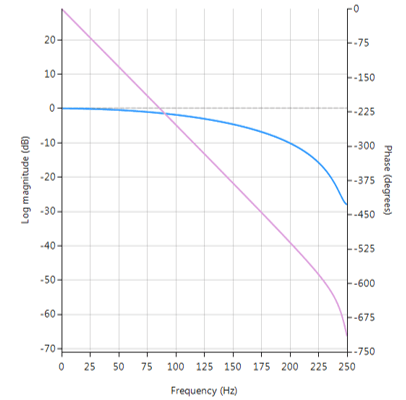
Frequency reponse of Farrow delay filter.
Implementatie
Een Farrow vertragingsfilter kan als volgt in ASN FilterScript worden geïmplementeerd :
[code language=”java”]
ClearH1; // clear primary filter from cascade
interface alpha = {0,1,0.02,.5}; // fractional delay
interface D = {1,30,1,10}; // integer delay
Main()
Num = {zeros(D),1-alpha,alpha}; // numerator coefficients
Den = {1}; // denominator coefficient
Gain = 1/sum(Num); // normalise gain at DC
[/code]
Kamfilters (Combfilters) worden gebruikt als powerline (50/60Hz) harmonische annuleringsfilters in audiotoepassingen, en vormen de basis van zogenaamde CIC (cascaded integrator-comb) filters. Deze worden gebruikt voor anti-aliasing in decimatie (sample rate reductie), en anti-imaging in interpolatie (sample rate toename) toepassingen.
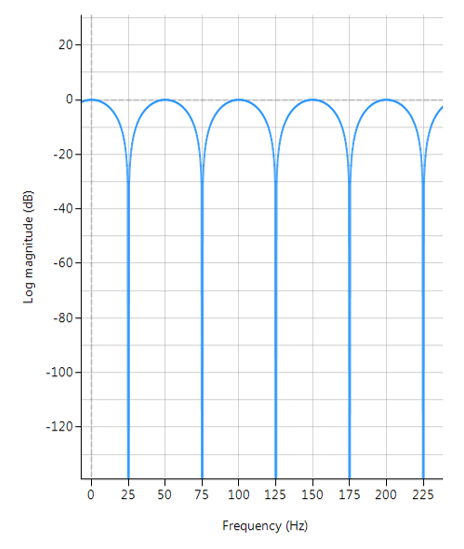
De frequentierespons van een kamfilter bestaat uit een reeks van op regelmatige afstand van elkaar geplaatste dalen, die het uiterlijk van een kam geven. Zoals te zien in onderstaande grafiek, verschijnt de afstand van elk dal op oneven of zelfs harmonisch van de gewenste grondfrequentie.
Frequentierespons van een typische FIR-kamfilter (oneven harmonieën):
\(f_s=500Hz\), \(f_c=25Hz\), \(L=10\) and \(\alpha=1\)
Een FIR-kamfilter kan worden beschreven met de volgende transferfunctie:
\(H(z)=1+\alpha z^{-L}\)
\(\Rightarrow Y(z)=X(z)\left[1+\alpha z^{-L}\right]\)
Het is duidelijk dat de kamfilter gewoon een gewogen vertraagde replica van zichzelf is, gespecificeerd door \(L\). Door het nemen van inverse z-transformaties krijgen we de verschilvergelijking die nodig is voor de implementatie,
\(y(n)=x(n)+\alpha x(n-L)\)Waarbij \(\alpha\) wordt gebruikt om de Q (bandbreedte) van de notch in te stellen. Deze kan zowel positief als negatief zijn, afhankelijk van het soort frequentierespons dat nodig is. Negatieve waarden van \(\alpha\) hebben hun eerste dieptepunt bij DC en hun tweede dieptepunt bij de fundamentele frequentie. Het is duidelijk dat dit type kamfilter gebruikt kan worden om eventuele DC-componenten uit een gemeten golfvorm te verwijderen als dat nodig is. Alle volgende dalen verschijnen bij gelijkmatige harmonische tot en met de Nyquist-frequentie.
Aan de andere kant hebben positieve waardes van \(\alpha\) alleen op de fundamentele en oneven harmonische frequenties, en kan als zodanig niet worden gebruikt om eventuele DC-componenten te verwijderen.
Toepassing op storingsonderdrukking van de stroomlijn
De affectiviteit van het kamfilter is afhankelijk van de sampling frequency, \(f_s\), aangezien \(L\) alleen beperkt is tot gehele waarden. Ook is een relatie tussen \(f_s\), als \(L\), afhankelijk van het teken van \(\alpha\). In het kader van de in deze discussie besproken toepassing van de netbeëindiging zullen dus alleen positieve waarden van de harmonics in aanmerking worden genomen, aangezien we alleen oneven harmonics hoeven te annuleren.
Een simpele relatie om \(L\) te bepalen kan als volgt worden samengevat voor positieve waardes van\(\alpha\):
\(L=ceil\left( \large{\frac{f_s}{2f_c}}\right)\)Waarbij \(f_c\) het gewenste middelpunt is van de fundamentele notch frequentie. Op basis van deze uitdrukking kunnen we de sample frequentie herberekenen op dusdanige wijze dat \(f_c\) een echt veelvoud is van \(f_s\)
\(f_{snew}=2f_c L\)Voorbeeld van een kamfilter
Voor het hier besproken voorbeeld, d.w.z. \(f_s=500Hz\) en \(f_c=25Hz\), verkrijgen we \(L=10\). Echter, als \(f_c=60Hz\), zouden we \(L=5\) nodig hebben en een nieuwe sampling rate van \(600Hz\). Hoewel het interessant is om op te merken dat \(f_s=480Hz\) voor \(L=4\) ook voldoende zou zijn.
Implementatie
Een FIR kamfilter kan als volgt in ASN FilterScript worden geimplementeerd:
ClearH1; // clear primary filter from cascade
interface L = {4,20,1,5}; // delay
interface alpha = {-1,1,0.01,1};
Main()
Num = {1,zeros(L-1),alpha}; // numerator coefficients
Den = {1};
Gain = 1/sum(abs(Num));
All-pass filters
All-pass filters bieden een eenvoudige manier om de faserespons van een IIR te wijzigen of te verbeteren zonder de omvang ervan te beïnvloeden. Als zodanig worden ze meestal aangeduid als fase-equalizers en hebben ze een bijzondere toepassing gevonden in digitale audiotoepassingen.
In zijn eenvoudigste vorm kan een filter worden opgebouwd uit een eerste orde transfer functie:
\( A(z)=\Large{\frac{r+z^{-1}}{1+r z^{-1}}} \, \, \normalsize{; r<1} \)
Merk bij \(\small A(z)\) op, dat de pool en de nul op de echte z-vlakas liggen en dat de pool bij de radius \(\small r\) een nul bij radius \(\small 1/r\) heeft. Zodanig dat de polen en nullen wederkerig zijn met elkaar. Deze eigenschap is de sleutel tot het all-pass filterconcept. Zoals we nu zullen zien door het concept verder uit te breiden naar een tweede orde all-pass filter:
\( A(z)=\Large\frac{r^2-2rcos \left( \frac{2\pi f_c}{fs}\right) z^{-1}+z^{-2}}{1-2rcos \left( \frac{2\pi f_c}{fs}\right)z^{-1}+r^2 z^{-2}} \)
Waarbij \(\small f_c\) de middenfrequentie is, \(\small r\) de radius of van de polen is en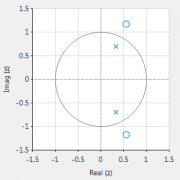 
\(\small f_s\) de sampling frequency. Merk op dat de teller en noemer coefficienten zijn weergegeven als
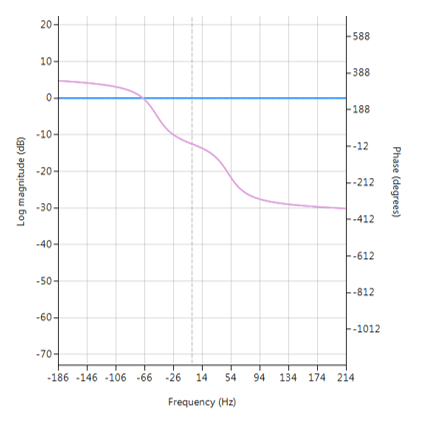Frequentierespons van het all-pass filter:
Let op de constante omvang van het spectrum (weergegeven in blauw).
Implementatie
Een All-pass filter kan geimplementeerd worden in ASN FilterScript als volgt:
[code language=”java”]
ClearH1; // clear primary filter from cascade
interface radius = {0,2,0.01,0.5}; // radius value
interface fc = {0,fs/2,1,fs/10}; // frequency value
Main()
Num = {radius^2,-2*radius*cos(Twopi*fc/fs),1};
Den = reverse(Num); // mirror image of Num
Gain = 1;
[/code]
Voor een gedetailleerde beschrijving van de IIR-faseregelaar en de APF (all-pass filter) ontwerptool van de ASN-filterontwerper, zie het volgende artikel.
Ingenieurs zijn tegenwoordig in staat met behulp van moderne embedded processors, softwareframeworks en design tooling geavanceerde meetconcepten toe te passen. Een van deze toepassingen zijn slimme fabrieken als onderdeel van de I4.0 revolutie.
De laatste jaren heeft PM (predictief onderhoud) van machines veel aandacht gekregen, waarbij fabrieken hun productie-efficiëntie willen maximaliseren. Tegelijkertijd willen zij de waardevolle vaardigheden van ervaren voormannen en productiemedewerkers behouden.
Traditioneel liep een voorman rond op de werkvloer en luisterde naar de geluiden die een machine maakte. Zo kreeg hij een idee waar mogelijk een verstoring zou plaats vinden. Met de komst van I4.0 technologie kunnen nu microfoons, edge DSP-algoritmes en ML worden ingezet. Deze ‘luisteren’ naar de geluiden die een machine maakt en maken vervolgens een classificatie en voorspelling.
Een van de grootste uitdagingen is hoe je een computer kunt laten horen als een mens.
Fysica van het menselijk oor
Een illustratie van het menselijk oor staat hiernaast weergegeven. Zoals te zien, is de basistaak van het oor het vertalen van geluid (luchttrilling) naar elektrische zenuwimpulsen die de hersenen kunnen interpreteren.
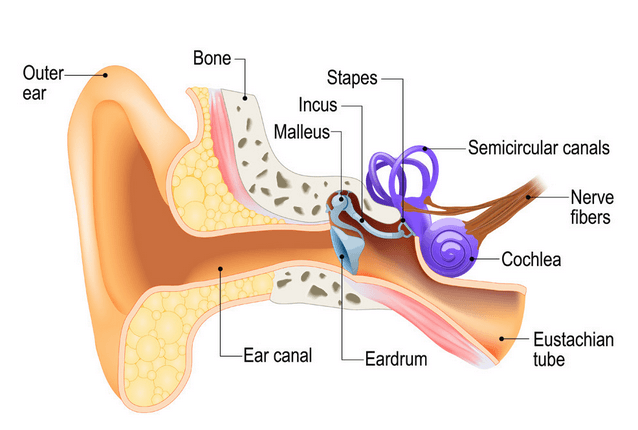
Hoe werkt het oor?
Het oor verwezenlijkt dit via drie botten (Stapes, Incus en Malleus) die fungeren als een mechanische versterker voor trillingen die worden ontvangen op het trommelvlies. Deze versterkte geluiden worden vervolgens via het Ovale venster (niet afgebeeld) naar het Cochlea gestuurd. De Cochlea (in paars weergegeven) is gevuld met een vloeistof die beweegt als reactie op de trillingen van het ovale venster. Als de vloeistof beweegt, worden duizenden zenuwuiteinden in beweging gezet. Deze zenuwuiteinden zetten geluidstrillingen om in elektrische impulsen die langs de auditieve zenuwvezels naar de hersenen gaan voor analyse.
Het modelleren van waargenomen geluid
Door de complexiteit van de vloeiende mechanische constructie van het menselijke auditieve systeem zijn lage en hoge frequenties doorgaans niet waarneembaar. Onderzoekers hebben in de loop der jaren ontdekt dat de mens het meest gevoelig is voor geluiden die in het 1-6kHz-bereik liggen. Daarbij varieert dit bereik, afhankelijk van de fysieke gezondheid van de proefpersoon.
Dit onderzoek heeft geleid tot de definitie van een set weighting curves (weegkrommes): de zogenaamde A-, B-, C- en D-weging curves, die de frequentierespons van een microfoon egaliseert. Deze weging curves hebben als doel de digitale en fysieke wereld dichter bij elkaar te brengen door een geautomatiseerd microfoonsysteem te laten horen als een mens.
De A-weging curve is de meest gebruikte, omdat deze volgens IEC-61672 op alle geluidsniveaumeters moet worden gemonteerd. De B- en D-curves worden nauwelijks gebruikt, maar de C-weging kan worden gebruikt voor het testen van de impact van geluid in telecomsystemen.
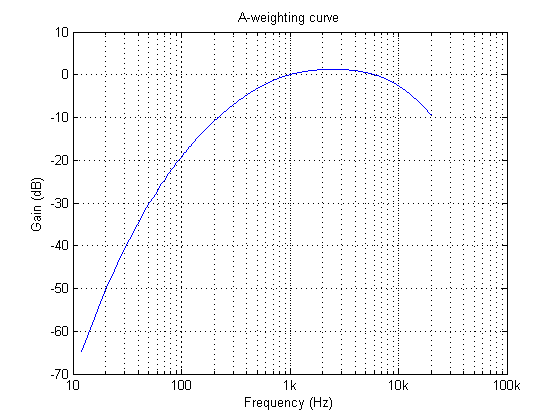
In bovenste grafiek is de frequentierespons van de A-weging curve weergegeven. De geluiden die onze oren onder 500Hz binnenkomen zijn gedefragmenteerd. Het best waarneembaar is tussen de 0.5-6kHz. Merk op dat de curve niet gespecificeerd is boven 20kHz, omdat dit het menselijke gehoorbereik overschrijdt.
ASN FilterScript
Met ASN’s FilterScript symbolische wiskunde scripttaal kunnen ontwerpers analoge filtertransferfuncties met slechts enkele regels code omzetten naar het digitale equivalent.
De analoge overdrachtsfuncties van de A- en C-weging curves staan hieronder vermeld:
\(H_A(s) \approx \displaystyle{7.39705×10^9 \cdot s^4 \over (s + 129.4)^2\quad(s + 676.7)\quad (s + 4636)\quad (s + 76655)^2}\)
\(H_C(s) \approx \displaystyle{5.91797×10^9 \cdot s^2\over(s + 129.4)^2\quad (s + 76655)^2}\)
Deze analoge transfer functies kunnen worden getransformeerd naar hun digitale equivalent door de bilinear() functie. Merk daarbij echter op dat \(H_A(s) \) een aanzienlijke hoeveelheid algebraïsche manipulatie vereist om de noemer van de coëfficiënten in machten van \(s\) te kunnen extraheren.
Convolutie
Een eenvoudige truc om polynomiale vermenigvuldiging uit te voeren is het gebruik van lineaire convolutie, wat dezelfde algebraïsche operatie is als het vermenigvuldigen van twee polynomialen samen. Dit kan eenvoudig worden uitgevoerd via Filterscript’s conv() functie:
y=conv(a,b);
Als eenvoudig voorbeeld: de vermenigvuldiging van \((s^2+2s+10)\) met \((s+5)\), wordt met 3 regels of FilterScript code gedefinieerd:
a={1,2,10};
b={1,5};
y=conv(a,b);
Dit geeft de volgende opbrengsten: 1 7 20 50 of \((s^3+7s^2+20s+50)\)
Voor de A-weging curve Laplace-transferfunctie wordt hieronder de volledige FilterScript-code gegeven:
ClearH1; // clear primary filter from cascade
Main() // main loop
a={1, 129.4};
b={1, 676.7};
c={1, 4636};
d={1, 76655};
aa=conv(a,a); // polynomial multiplication
dd=conv(d,d);
aab=conv(aa,b);
aabc=conv(aab,c);
Na=conv(aabc,dd);
Nb = {0 ,0 , 1 ,0 ,0 , 0, 0}; // define numerator coefficients
G = 7.397e+09; // define gain
Ha = analogtf(Nb, Na, G, "symbolic");
Hd = bilinear(Ha,0, "symbolic");
Num = getnum(Hd);
Den = getden(Hd);
Gain = getgain(Hd)/computegain(Hd,1e3); // set gain to 0dB@1kHz
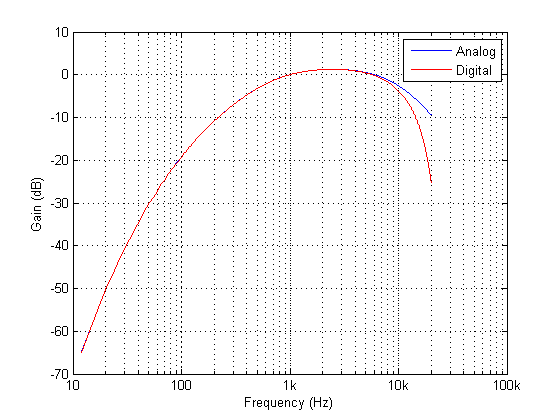
Zoals te zien is, komt de digitale equivalente magnitudereactie zeer nauw overeen met de ideale analoge magnitudereactie tot \(6kHz\).
De ITU-R 486–4 weging curve
Een andere belangrijke wegingcurve is de ITU-R 486–4 weighting curve. Deze is ontwikkeld door de BBC. In tegenstelling tot het A-weging curve filter beschrijft de ITU-R 468-4-curve de subjectieve luidheid voor breedbandstimuli. Het belangrijkste nadeel van de A-weging curve is dat deze de luidheidsevaluatie van reële stimuli onderschat, met name in de frequentieband van ongeveer 1-9 kHz.
Door de precieze definitie van de 486-4 wegingscurve is er geen analoge transfer functie beschikbaar. In plaats daarvan biedt de standaard een tabel met amplitudes en frequenties – hier weergegeven. Deze specificatie kan rechtstreeks worden ingevoerd in Filterscript’s firarb() functie om een geschikt FIR filter te ontwerpen, zie hieronder:
ClearH1; // clear primary filter from cascade
ShowH2DM;
interface L = {10,400,10,250}; // filter order
Main()
// ITU-R 468 Weighting
A={-29.9,-23.9,-19.8,-13.8,-7.8,-1.9,0,5.6,9,10.5,11.7,12.2,12,11.4,10.1,8.1,0,-5.3,-11.7,-22.2};
F={63,100,200,400,800,1e3,2e3,3.15e3,4e3,5e3,6.3e3,7.1e3,8e3,9e3,1e4,1.25e4,1.4e4,1.6e4,2e4};
A={-30,A}; // specify arb response
F={0,F,fs/2}; //
Hd=firarb(L,A,F,"blackman","numeric");
Num=getnum(Hd);
Den={1};
Gain=getgain(Hd);
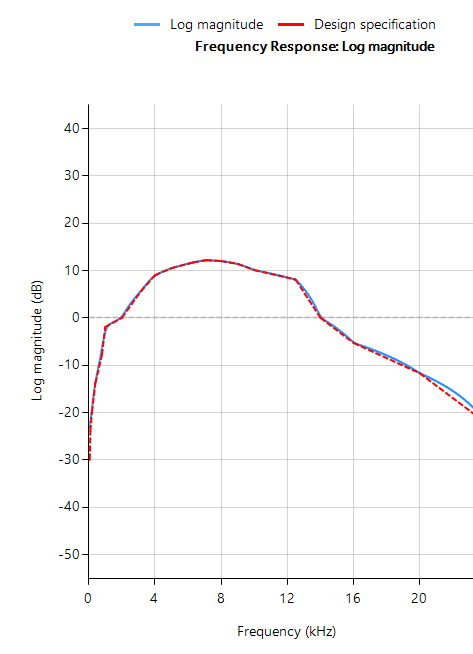
Frequentierespons van een ITU-R 468-4 FIR-filter ontworpen met Filterscript’s firarb() functie voor \(f_s=48kHz\)
Zoals te zien, biedt FilterScript de ontwerper een zeer krachtige symbolische scripttaal voor het ontwerpen van weeg curve filters. Nu volgt een bespreking van de implementatie van een A-weeg curve filter op een Arm gebaseerde processor via de automatische codegenerator van de tool. De concepten en stappen die hieronder worden gedemonstreerd gelden ook voor FIR-filters.
Automatische code generatie naar Arm processor cores via CMSIS-DSP
Het filter ontwerp kan nu met de automatische codegeneratie-engine van de ASN Filter Designer nu geexporteerd worden naar een Cortex-M Arm-gebaseerde processor via het CMSIS-DSP software raamwerk. De ingebouwde analyse- en helpfuncties van de tool helpen de ontwerper bij het succesvol configureren van het ontwerp voor implementatie.
Voordat de code wordt gegenereerd, moet het H2-filter (d.w.z. het filter dat in FilterScript is ontworpen) eerst opnieuw worden geoptimaliseerd (getransformeerd) naar een H1-filter (hoofdfilter) structuur voor gebruik. Het optiemenu is te vinden onder de P-Z tab in de hoofd UI.
Alle ontwerpen van IIR-filters met floating point moeten gebaseerd zijn op Single Precision arithmetic en ofwel een Direct Form I of Direct Form II getransponeerde filterstructuur hebben. De Direct Form II getransponeerde structuur wordt geadviseerd voor floating point implementatie vanwege de hogere numerieke nauwkeurigheid.
De instellingen voor kwantisatie en de filterstructuur zijn te vinden onder het tabblad Q (zoals links afgebeeld). Door Arithmetic op Single Precision te zetten en Structure op Direct Form II Transposed en vervolgens op Apply te klikken, wordt de IIR voor het CMSIS-DSP software raamwerk geconfigureerd.
Selecteer het Arm CMSIS-DSP raamwerk in het selectievakje in het filteroverzichtsvenster:
De automatisch gegenereerde C-code op basis van het CMSIS-DSP framework voor directe implementatie op een Arm-gebaseerde Cortex-M processor staat hieronder weergegeven:
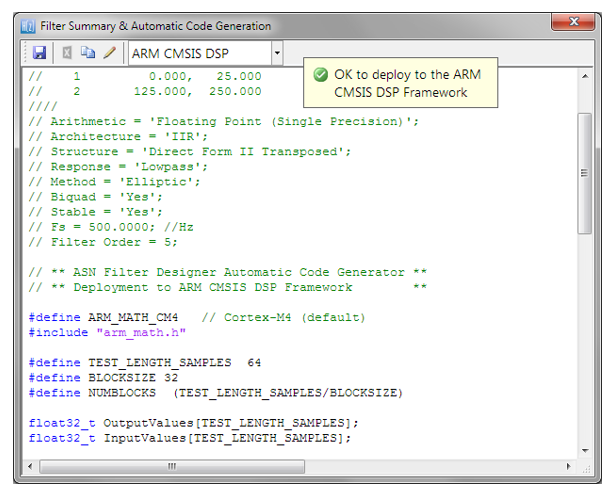
Zoals weergegeven, genereert de automatische codegenerator van de ASN Filter Designer alle initialisatiecode, schaling en datastructuren die nodig is om het A-weighting IIR-filter te implementeren via de CMSIS-DSP-bibliotheek van Arm.
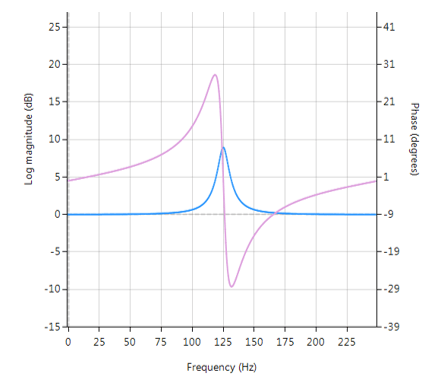
Een Peaking of Bell filter is een type geluidsequalisatiefilter dat de grootte van een bepaalde set frequenties rond een centrumfrequentie versterkt of verzwakt om zo de magnitude van het geluid te egaliseren. Zoals te zien is in de grafiek hieronder, ontleent het filter zijn naam aan de vorm van het magnitudenspectrum (blauwe lijn) dat lijkt op een Bell-curve.
Frequentierespons (magnitude weergegeven in blauw, fase weergegeven in paars) van een 2e orde Bell-filter met een piek bij 125 Hz
All-pass filters
Centraal in het Bell-filter staat het zogenaamde All-pass filter. All-pass filters bieden een eenvoudige manier om de faserespons van een IIR te wijzigen/verbeteren zonder de grootte van de IIR te beïnvloeden. Als zodanig worden ze meestal aangeduid als fase-equalizers en hebben ze een bijzondere toepassing gevonden in digitale audiotoepassingen.
Een tweede orde all-pass filter is gedefinieerd als:
\( A(z)=\Large\frac{r^2-2rcos \left( \frac{2\pi f_c}{fs}\right) z^{-1}+z^{-2}}{1-2rcos \left( \frac{2\pi f_c}{fs}\right)z^{-1}+r^2 z^{-2}} \)
Merk op hoe de teller- en noemercoëfficiënten in spiegelbeeldig van elkaar zijn gerangschikt. De eigenschap van dit spiegelbeeld is wat de all-pass filter zijn gewenste eigenschap geeft, namelijk de ontwerper in staat stellen om de faserespons te veranderen terwijl de magnituderespons constant of vlak blijft over het volledige frequentiespectrum.
Een Bell filter kan worden geconstrueerd uit de \(A(z)\) filter door de volgende transferfunctie:
\(H(z)=\Large\frac{(1+K)+A(z)(1-K)}{2}\)
Na enige algebraïsche vereenvoudiging krijgen we de transferfunctie voor de Peaking of Bell filter als:
\(H(z)=\Large{\frac{1}{2}}\left[\normalsize{(1+K)} + \underbrace{\Large\frac{k_2 + k_1(1+k_2)z^{-1}+z^{-2}}{1+k_1(1+k_2)z^{-1}+k_2 z^{-2}}}_{all-pass filter}\normalsize{(1-K)} \right] \)
- \(K\) wordt gebruikt om de gain en het teken van de piek in te stellen
- \(k_1\) stelt de piek middenfrequentie in
- \(k_2\) stelt de bandbreedte van de piek in
Implementatie
Een Bell filter kan gemakkelijk ASN FilterScript worden geimplementeerd:
ClearH1; // clear primary filter from cascade
interface BW = {0,2,0.1,0.5}; // filter bandwidth
interface fc = {0, fs/2,fs/100,fs/4}; // peak/notch centre frequency
interface K = {0,3,0.1,0.5}; // gain/sign
Main()
k1=-cos(2*pi*fc/fs);
k2=(1-tan(BW/2))/(1+tan(BW/2));
Pz = {1,k1*(1+k2),k2}; // define denominator coefficients
Qz = {k2,k1*(1+k2),1}; // define numerator coefficients
Num = (Pz*(1+K) + Qz*(1-K))/2;
Den = Pz;
Gain = 1;
Deze code kan nu gebruikt worden om een geschikt Bell filter te ontwerpen, waarbij de exacte waardes van \(K, f_c\) en \(BW\) gemakkelijk kunnen worden gevonden door de interface variabelen te tweaken waarbij het resultaat in real-time te zien is, zoals hieronder weergegeven.
Directe aanpassingen in filter ontwerp
Bij de interactiviteit van de FilterScript IDE (geïntegreerde ontwikkelomgeving) staan de zogenaamde interfacevariabelen centraal. Een interface variabele wordt eenvoudigweg genoemd: een scalaire invoervariabele die gebruikt kan worden om een symbolische expressie te wijzigen zonder dat de code opnieuw gecompileerd hoeft te worden – dit stelt ontwerpers in staat om ‘on the fly’ te ontwerpen en snel tot een optimale oplossing te komen.
Zoals in het codevoorbeeld hierboven te zien is, moeten de interfacevariabelen worden gedefinieerd in de initialisatiesectie van de code, en kunnen ze constanten (zoals fs and pi) en eenvoudige wiskundige operatoren, zoals vermenigvuldigen * en /delen, bevatten. Dit wanneer het toevoegen van functies aan een interfacevariabele niet wordt ondersteund.
Een interfacevariabele wordt gedefinieerd als een vectorexpressie:
interface name = {minimum, maximum, step_size, default_value};
Waarbij alle vermeldingen echte scalaire waarden moeten zijn. Vectoren en complexe waarden worden niet gecompileerd.
[arve mp4=”https://www.advsolned.com/wp-content/uploads/2018/07/peakingfilter.mp4″ align=”right” loop=”true” autoplay=”true” nodownload nofullscreen noremoteplayback… /]
Real-time updates
Alle interfacevariabelen worden gewijzigd via de interfacevariabele regelaar GUI. Na het compileren van de code gebruikt u de interface variabele controller om de waarden van de interface variabelen te tweaken en de effecten op de overdrachtsfunctie te zien. Als u test op live audio, kunt u een geladen audiobestand streamen en de interfacevariabelen in real-time aanpassen om de effecten van de nieuwe instellingen te horen.