Amélioration des conceptions existantes basées sur des filtres analogiques
Les filtres analogiques existent depuis les débuts de l’électronique, depuis les simples réseaux inductance-condensateur jusqu’aux filtres actifs plus avancés avec des amplificateurs opérationnels. En tant que tel, il existe une riche collection de conceptions de filtres une large gamme d’applications de mesure de capteurs. Cependant, avec les exigences de performance des applications modernes de mesure de capteurs IoT (Internet des objets) et la baisse des coûts des produits, les filtres numériques intégrés dans le code d’application du microcontrôleur deviennent la norme, (strong>mais comment obtenir le meilleur des deux mondes??
Plutôt que de réinventer la roue, les concepteurs de produits peuvent prendre une fonction de transfert de filtre analogique existante, la transformer en numérique (via une transformation) et l’implémenter en tant que filtre numérique dans un microcontrôleur ou un DSP (processeur de signal numérique). Bien que les transformations analogiques-numériques existent depuis des décennies, la disponibilité d’outils de conception de DSP permettant d’ajuster le “filtre numérique transformé” a été quelque peu limitée, ce qui a entravé le processus de conception et de validation.
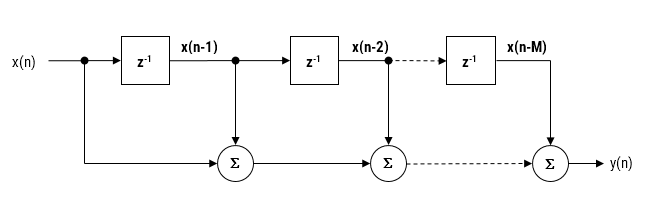
Un filtre passe-bas analogique de 2e ordre est illustré ci-dessous. Dans sa forme la plus simple, seuls 5 composants sont nécessaires pour construire le filtre, ce qui semble facile. N’est-ce pas?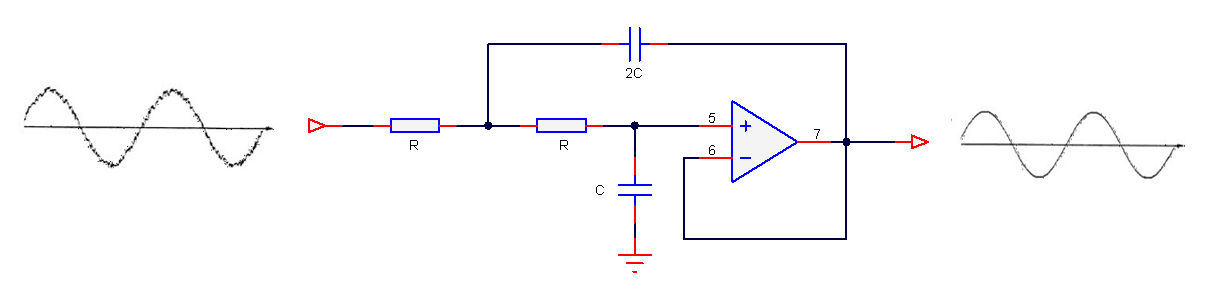
Les avantages
L’avantage le plus évident est que les filtres analogiques ont une excellente résolution, car il n’y a pas de “nombre de bits” à prendre en compte. Les filtres analogiques ont de bonnes propriétés CEM (compatibilité électromagnétique) car aucun bruit d’horloge n’est généré. Il n’y a pas d’effets de repliement, ce qui est certainement vrai pour les amplificateurs opérationnels plus simples, qui n’ont pas de circuit fantaisiste de hachage ou d’auto-calibrage intégré, et les conceptions analogiques peuvent être bon marché, ce qui est idéal pour les applications sensibles au coût.
C’est très bien, mais quelle est la mauvaise nouvelle ?
Les filtres analogiques présentent plusieurs inconvénients importants qui affectent leurs performances, tels que le vieillissement des composants, la dérive en température et la tolérance des composants. De plus, de bonnes performances exigent de bonnes compétences en matière de conception analogique et une bonne disposition des circuits imprimés, ce qui est difficile à trouver sur le marché actuel des compétences.
Ces inconvénients rendent les filtres numériques beaucoup plus attrayants pour les applications modernes, qui exigent une grande répétabilité des caractéristiques. Prenons un exemple : disons que vous souhaitez fabriquer 1000 modules de mesure après avoir optimisé la conception de votre filtre. Avec une solution numérique, vous pouvez être sûr que les performances de votre filtre seront identiques dans tous les modules. Ce n’est certainement pas le cas avec l’analogique, car la tolérance des composants, leur vieillissement et la dérive de la température font que le filtre de chaque module aura ses propres caractéristiques. De plus, la réponse en fréquence d’un filtre analogique reste fixe, c’est-à-dire qu’un filtre de Butterworth sera toujours un filtre de Butterworth – toute modification de la réponse en fréquence nécessiterait de changer physiquement les composants sur le circuit imprimé – ce qui n’est pas idéal !
Les filtres numériques sont adaptatifs et flexibles, nous pouvons concevoir et mettre en œuvre un filtre avec la réponse en fréquence que nous voulons, le déployer et mettre à jour les coefficients du filtre sans rien changer sur le PCB ! Il est également facile de concevoir des filtres numériques avec une phase linéaire et à des fréquences d’échantillonnage très basses – deux choses qui sont délicates avec l’analogique.
Transformations de Laplace en transformées discrètes/numériques
Les trois méthodes présentées ici consistent essentiellement à transformer une fonction de transfert de Laplace (analogique), \(H(s)\), en une fonction de transfert discrète, \(H(z)\), de sorte qu’un filtre analogique éprouvé et déjà utilisé dans une conception puisse être mis en œuvre sur un microcontrôleur ou un DSP.
Une sélection de quelques transformées de Laplace en z utiles est donnée dans le tableau ci-dessous :
\(
\begin{array}{ccc}\hline
H(s) &\longleftrightarrow & H(z) \\ \hline
1 &\longleftrightarrow & 1 \\
\frac{\displaystyle1}{\displaystyle s}
&\longleftrightarrow& \frac{\displaystyle 1}{\displaystyle 1-z^{\scriptstyle -1}}\\
\frac{\displaystyle 1}{\displaystyle s^{\scriptstyle 2}} &\longleftrightarrow& \frac{\displaystyle
Tz^{\scriptstyle-1}}{\displaystyle (1-z^{\scriptstyle -1})^2}\\
\frac{\displaystyle 1}{\displaystyle s+a}
&\longleftrightarrow&
\frac{\displaystyle 1}{\displaystyle 1-e^{-aT}z^{-1}}\\
\frac{\displaystyle 1}{\displaystyle (s+a)^2}
&\longleftrightarrow& \frac{\displaystyle z^{-1}(1-e^{-aT})}{\displaystyle a(1-z^{-1})(1-e^{-aT}z^{-1})}\\\hline
\end{array}
\)
Un tableau des transformées de Laplace et de z utiles
La transformée en z bilinéaire (BZT)
La transformée bilinéaire en z (BZT) convertit simplement une fonction de transfert analogique, \(H(s)\), en une fonction de transfert discrète, \(s\), en remplaçant tous les termes s par les suivants :
\(\displaystyle
s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} \label{bzt}\)
Où, \(T\) est la période d’échantillonnage du système discret. Cependant, en substituant \(s=j\Omega\) et \(z=e^{jwT}\) dans l’équation BZT et en simplifiant, on remarque qu’il existe en réalité une relation non linéaire entre les fréquences analogiques, \(\Omega\) et discrètes, \(w\). Cette relation est montrée ci-dessous, et est due à la non-linéarité de la fonction arctangente.
\(\displaystyle
\omega=2\tan^{-1}\left(\frac{\Omega T}{2}\right)
\label{bzt_warp_def1}
\)
En analysant l’équation, on constate que les fréquences analogiques équidistantes dans la plage \(-\infty<\Omega<\infty\) sont compressées de manière non linéaire dans la plage de fréquences \(-\pi<w<\pi\) dans le domaine discret. Cette relation est appelée déformation des fréquences, et peut être compensée par une déformation préalable des fréquences analogiques par:
\(\displaystyle
\Omega_c=\frac{2}{T}\tan\left(\frac{\Omega_d T}{2}\right)
\label{bzt_warp_def2}
\)
où, \(\displaystyle\Omega_c\) est la fréquence analogique compensée ou pré-gauchie, et \(\displaystyle\Omega_d\) est la fréquence analogique souhaitée.
La commande \(\texttt{bilinear}\) de ASN FilterScript peut être utilisée pour convertir une fonction de transfert de Laplace en son équivalent discret en utilisant la transformée BZT. Un exemple est donné ci-dessous. La commande ASN FilterScript bilinéaire peut être utilisée pour convertir une fonction de transfert Laplace en son équivalent discret en utilisant la transformée BZT. Un exemple est donné ci-dessous.
La transformation invariante en fonction des impulsions
La deuxième transformation est appelée transformation invariante aux impulsions (IIT), car les pôles de la fonction de transfert de Laplace sont convertis en leurs équivalents discrets, de sorte que la réponse impulsionnelle discrète, \(h(n)\), est identique à une représentation régulièrement échantillonnée de la réponse impulsionnelle analogique (c’est-à-dire \(h(n)=h(nT)\), où \(T\) est le taux d’échantillonnage et \(t=nT\)). L’IIT est une technique de transformation beaucoup plus fastidieuse que la BZT, car la fonction de transfert de Laplace doit d’abord être développée à l’aide de fractions partielles avant d’appliquer la transformation.
La technique de transformation est définie ci-dessous:
\(\displaystyle
\frac{K}{s+a} \quad\longrightarrow\quad
\frac{K}{1-e^{-aT}z^{-1}} \label{iit_def}
\)
Cette méthode souffre de plusieurs contraintes, puisqu’elle ne permet pas la transformation des zéros ou des termes constants individuels (une fois développés), et doit avoir un taux d’échantillonnage élevé afin de surmonter les effets de l’aliasing spectral. En effet, les effets de repliement gênent considérablement cette méthode, de sorte qu’elle ne devrait être utilisée que lorsque l’exigence est de faire correspondre la réponse impulsionnelle de la fonction de transfert analogique, puisque le modèle discret résultant peut avoir un spectre d’amplitude et de phase (réponse en fréquence) différent de celui du système analogique original. Par conséquent, la méthode d’invariant d’impulsion ne convient pas à la modélisation des filtres passe-haut, et est donc limitée à la modélisation des filtres de type passe-bas ou passe-bande.
En raison des limitations susmentionnées de la méthode IIT, elle n’est actuellement pas supportée dans ASN Filterscript.
La transformation Matched-z
Une autre technique de modélisation analogique à discrète est la transformation matched-z. Comme son nom l’indique, cette transformation convertit les pôles et les zéros de la fonction de transfert analogique directement en pôles et zéros dans le plan z. La transformation est décrite ci-dessous, où \(T\) est la fréquence d’échantillonnage.
\(\displaystyle
\frac{\prod\limits_{k=1}^q(s+b_k)}{\prod\limits_{k=1}^p(s+a_k)}
\quad\longrightarrow\quad
\frac{\prod\limits_{k=1}^q(1-e^{-b_kT}z^{-1})}{\prod\limits_{k=1}^p(1-e^{-a_kT}z^{-1})}
\label{matchedz_def}
\)
En analysant l’équation de transformation, on constate que les pôles transformés du plan z seront identiques aux pôles obtenus avec la méthode de l’invariant d’impulsion. Cependant, notez que les positions des zéros seront différentes, puisque la méthode de l’invariant d’impulsion ne peut pas les transformer.
La commande ASN Filterscript \(\texttt{mztrans}\) est disponible pour cette méthode.
Un exemple détaillé
Afin de démontrer la facilité de transformer les filtres analogiques en leurs équivalents discrets/numériques à l’aide des transformées analogiques/discrètes, un exemple de modélisation avec la BZT va maintenant suivre pour un filtre analogique passe-bas du 2ème ordre.
Un filtre analogique passe-bas d’ordre 2 généralisé est donné par:
\(\displaystyle
H(s)=\frac{w_c^2}{s^2+2\zeta w_c s + w_c^2}
\)
Où \(w_c=2\pi f_c\) est la fréquence de coupure et \(\zeta\) définit l’amortissement du filtre, où un \(\zeta=1/\sqrt{2}\) est dit être amorti de façon critique ou égal à -3dB à \(w_c\). De nombreux ingénieurs analogiques choisissent de spécifier un facteur de qualité, \(Q = \displaystyle\frac{1}{2\zeta}\) ou un facteur de crête pour leurs conceptions. En substituant \(Q\) dans \(H(s)\), nous obtenons :
\(\displaystyle
H(s)=\frac{w_c^2}{s^2+ \displaystyle{\frac{w_c}{Q}s} + w_c^2}
\)
En analysant \(H(s)\), on remarque que \(Q=1/\sqrt{2} = 0.707\) donne également une réponse amortie de façon critique. Différentes valeurs de \(Q\) sont illustrées ci-dessous, et comme on le voit lorsque \(Q>1/\sqrt{2}\) un pic se produit.
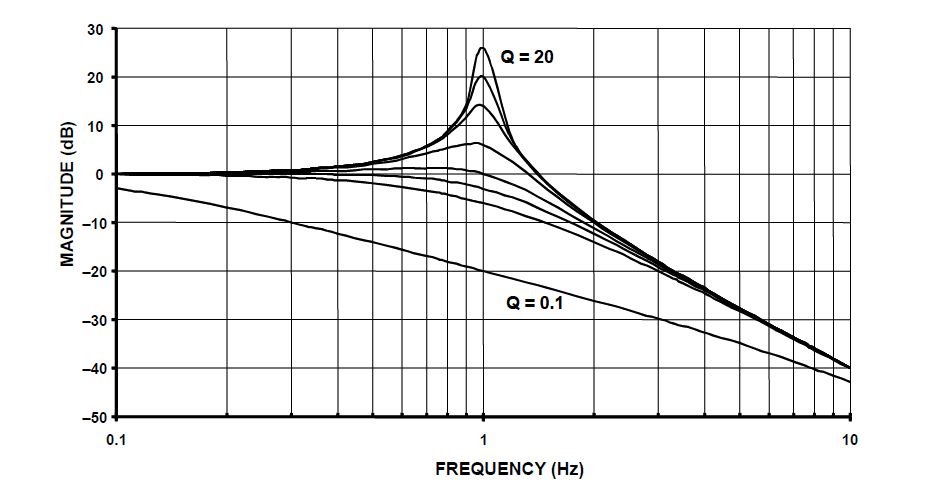
Spectre d’amplitude du prototype du filtre passe-bas du 2ème ordre pour différentes valeurs de Q:
remarquez que lorsque \(Q>1/\sqrt{2}\) un pic se produit.
Avant d’appliquer la BZT dans ASN FilterScript, la fonction de transfert analogique doit être spécifiée dans un objet filtre analogique. Le code suivant configure un objet filtre analogique pour le prototype passe-bas d’ordre 2 considéré ici :
Main()
wc=2*pi*fc;
Nb={0,0,wc^2};
Na={1,wc/Q,wc^2};
Ha=analogtf(Nb,Na,1,"symbolic"); // make analog filter object
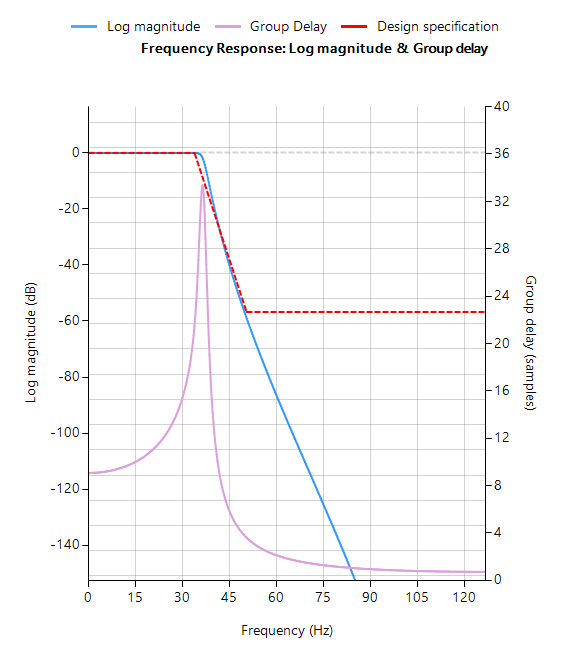
Le mot clé \(\texttt{symbolic}\) génère une représentation symbolique de la fonction de transfert dans la fenêtre de commande. Pour un taux d’échantillonnage de \(f_s=500Hz\) et \(f_c=30Hz\) et \(Q=0.707\), on obtient :

Application de la BZT via la commande \(\texttt{bilinear}\) sans préwarping,
Hd=bilinear(Ha,0,"symbolic");

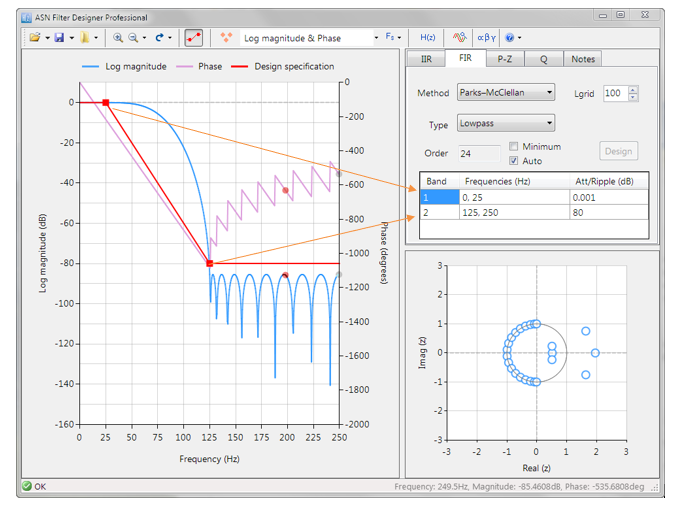
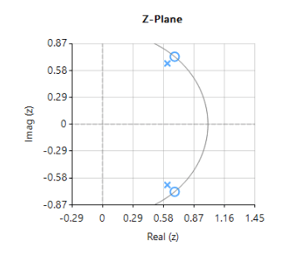
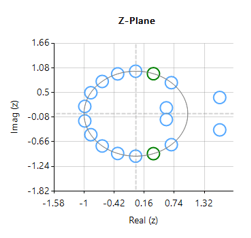
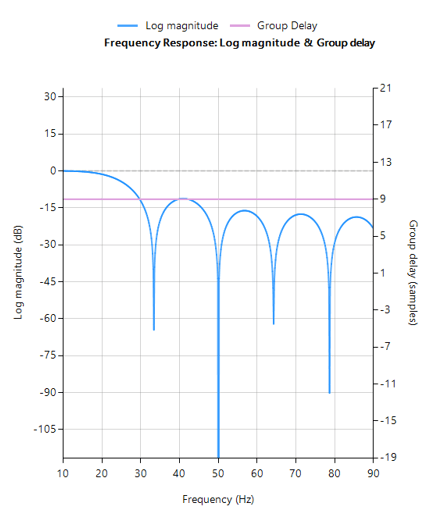
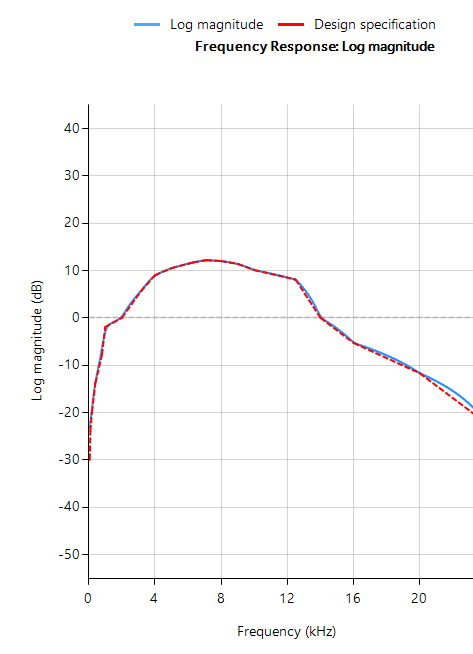
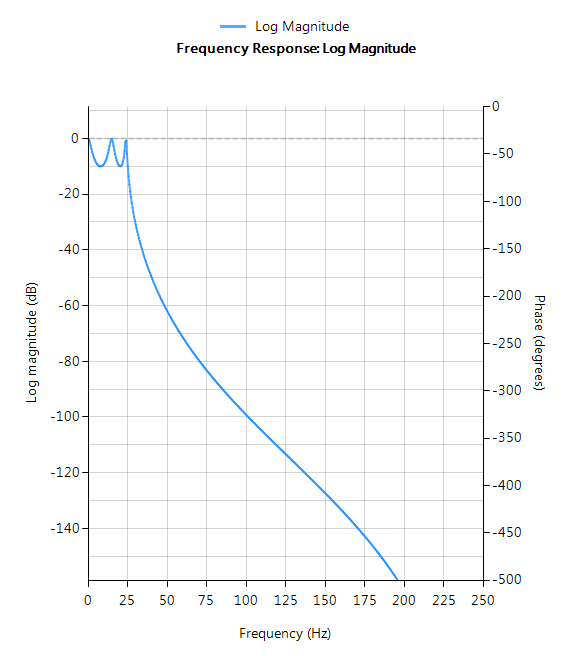
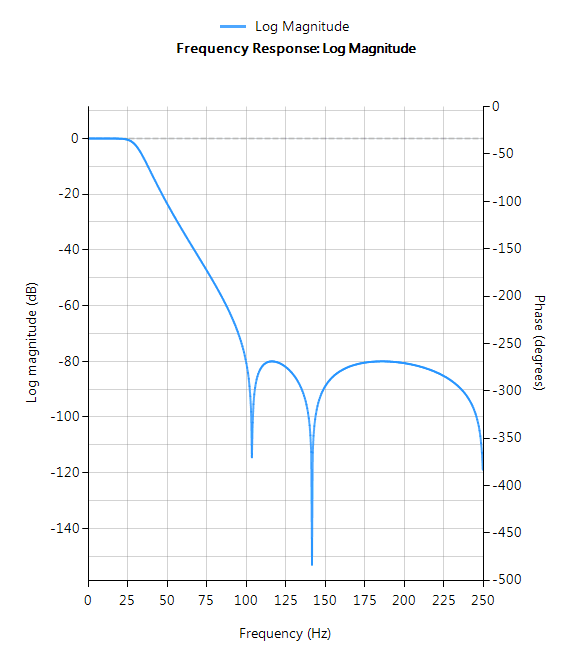
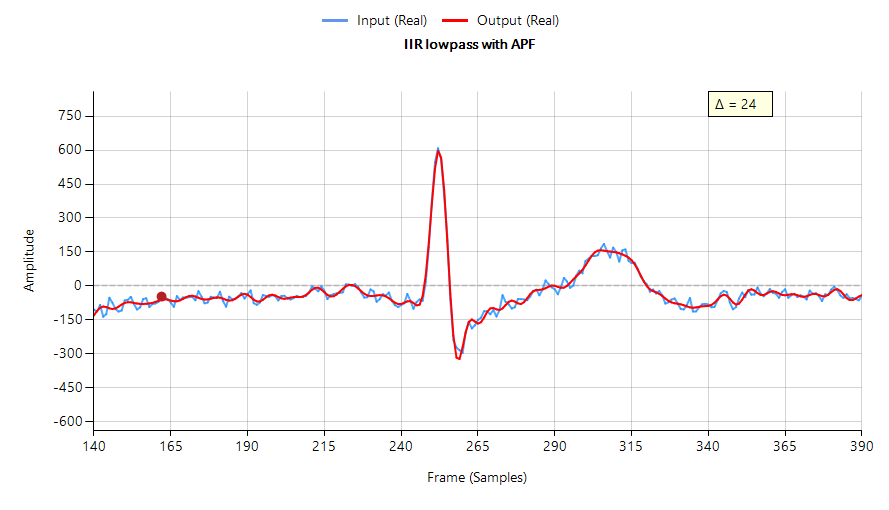
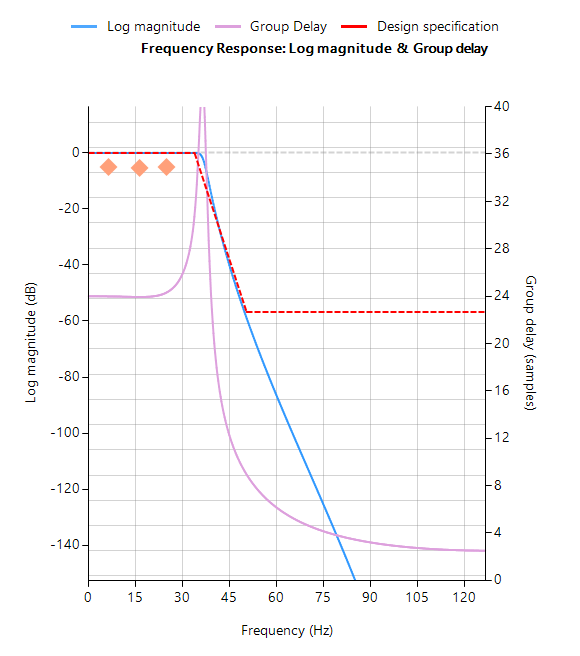
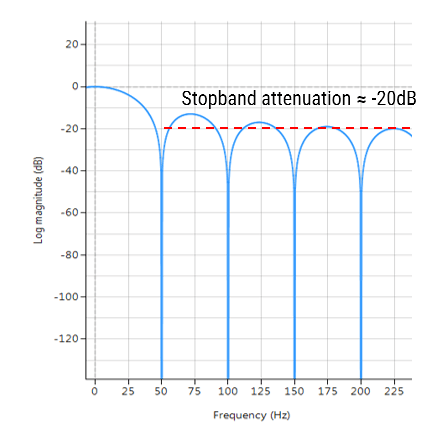
La réponse en fréquence complète du filtre numérique transformé est présentée ci-dessous, où l’on peut voir qu’à \(30Hz\), l’amplitude est de \(-3dB\) et la phase de \( -90^{\circ}\), ce qui est conforme aux attentes. Remarquez également comment l’atténuation de la magnitude du filtre est affectée par la double paire de zéros à Nyquist (voir le graphique du plan z ci-dessous), ce qui entraîne des différences avec son cousin analogique. 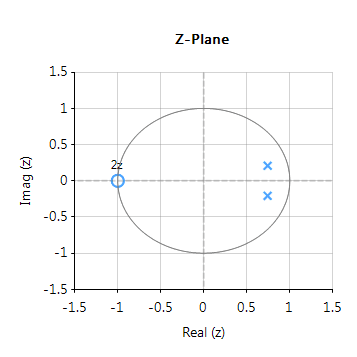
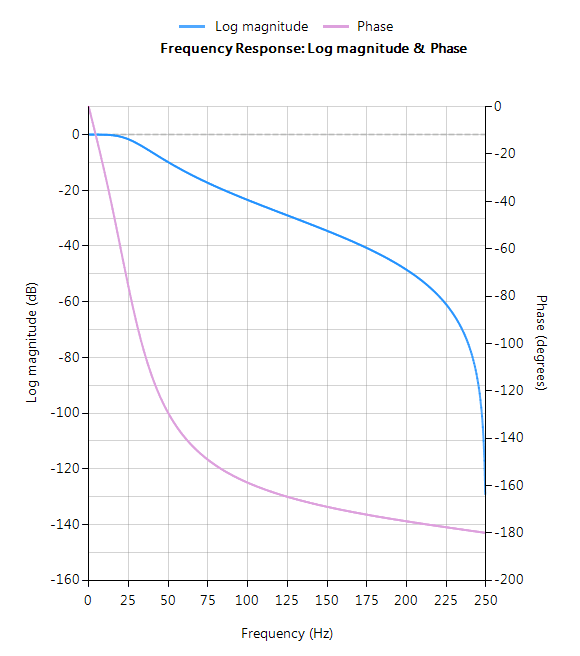
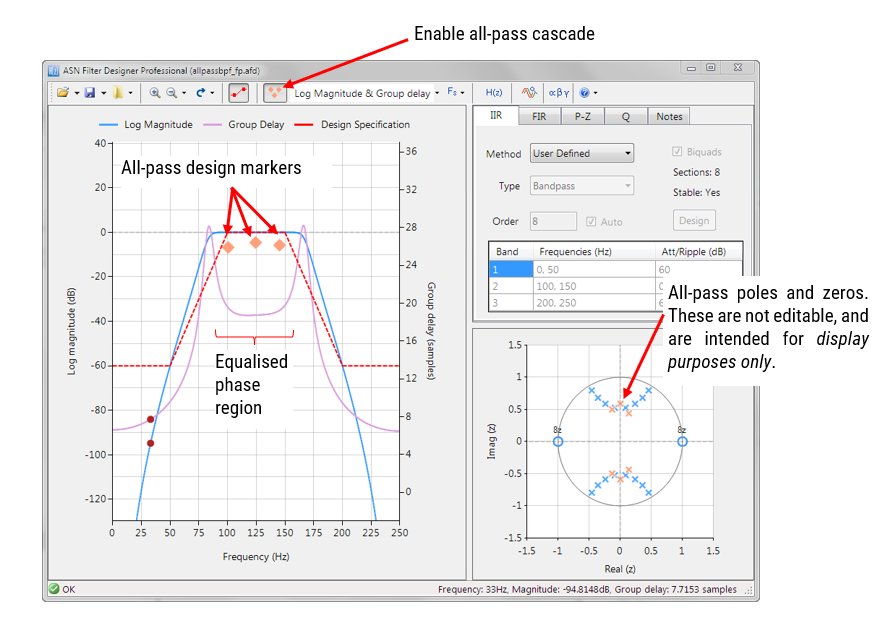
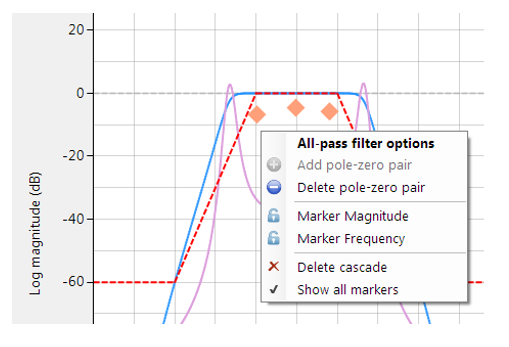
Les positions des pôles et des zéros peuvent être modifiées dans ASN Filterscript ou via l’éditeur interactif du plan z des pôles et des zéros de ASN Filter Designer en utilisant simplement la souris!
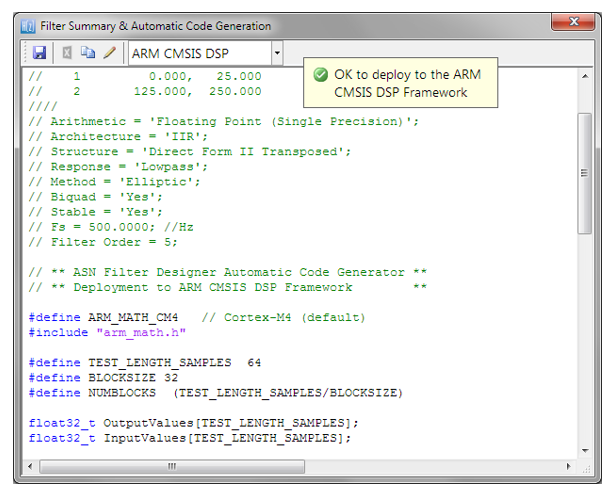
Implémentation
Le code complet pour transformer un prototype de filtre passe-bas analogique généralisé du 2ème ordre en son équivalent numérique en utilisant le BZT via ASN FilterScript est donné ci-dessous :
ClearH1; // clear primary filter from cascade
interface Q = {0.1,10,0.02,0.707};
interface fc = {10,200,10,40};
Main()
wc=2*pi*fc;
Nb={0,0,wc^2};
Na={1,wc/Q,wc^2};
Ha=analogtf(Nb,Na,1,"symbolic"); // make analog filter object
Hd=bilinear(Ha,0,"symbolic"); // transform Ha via BZT into digital object, Hd
Num=getnum(Hd);
Den=getden(Hd);
Gain=getgain(Hd);

Download demo now
Licencing information