Filter mit unendlicher Impulsantwort (IIR) sind für eine Vielzahl von Sensormessanwendungen nützlich, einschließlich der Entfernung von Messrauschen und der Unterdrückung unerwünschter Komponenten, wie z. B. Stromleitungsstörungen. Obwohl mehrere praktische Implementierungen für den IIR existieren, bietet die Struktur Direct form II Transposed die beste numerische Genauigkeit für die Fließkomma-Implementierung. Wenn jedoch eine Festkomma-Implementierung auf einem Mikrocontroller in Betracht gezogen wird, gilt die Struktur Direkte Form I aufgrund ihres großen Akkumulators, der eventuelle Zwischenüberläufe aufnimmt, als die beste Wahl. Diese Application Note befasst sich speziell mit dem Entwurf und der Implementierung von IIR-Biquad-Filtern auf einem Cortex-M-basierten Mikrocontroller mit dem ASN Filter Designer sowohl für Fließkomma- als auch für Festkomma-Anwendungen über das Arm CMSIS-DSP Software-Framework.
Es werden auch Details (einschließlich eines Referenzbeispielprojekts) zur Implementierung des IIR-Filters in Arm/Keils MDK-Industriestandard-Cortex-M-Mikrocontroller-Entwicklungskit gegeben.
Einführung
ASN Filter Designer bietet Ingenieuren eine leistungsfähige DSP-Experimentierplattform, die den Entwurf, das Experimentieren und den Einsatz komplexer IIR- und FIR (Finite Impulse Response)-Digitalfilterdesigns für eine Vielzahl von Sensormessanwendungen ermöglicht. Die fortschrittliche Funktionalität des Tools umfasst einen grafikbasierten Echtzeit-Filterdesigner, mehrere Filterblöcke, verschiedene mathematische I/O-Blöcke, symbolisches Live-Mathe-Scripting und Echtzeit-Signalanalyse (über einen integrierten Signalanalysator). Diese Vorteile in Verbindung mit der automatischen Dokumentation und Code-Generierungsfunktionalität ermöglichen es Ingenieuren, ein digitales Filter innerhalb von Minuten statt Stunden zu entwerfen und zu validieren.
Das Arm CMSIS-DSP (Cortex Microcontroller Software Interface Standard) Software-Framework ist eine reichhaltige Sammlung von über sechzig DSP-Funktionen (einschließlich verschiedener mathematischer Funktionen wie Sinus und Kosinus; IIR/FIR-Filterfunktionen, komplexe mathematische Funktionen und Datentypen), die von Arm entwickelt und für die Cortex-M-Prozessorkerne optimiert wurden.

Das Framework macht ausgiebig Gebrauch von hoch optimierten SIMD-Befehlen (Single Instruction, Multiple Data), die mehrere identische Operationen in einem einzigen Befehlszyklus ausführen. Die SIMD-Befehle (sofern vom Core unterstützt) in Verbindung mit anderen Optimierungen ermöglichen es Ingenieuren, schnell und einfach hochoptimierte Signalverarbeitungsanwendungen für Cortex-M-basierte Mikrocontroller zu erstellen.
Der ASN Filter Designer unterstützt das CMSIS-DSP Software-Framework vollständig, indem er über seine Code-Generierungs-Engine automatisch optimierten C-Code auf Basis der DSP-Funktionen des Frameworks erzeugt.
Entwurf von IIR-Filtern mit dem ASN Filter Designer
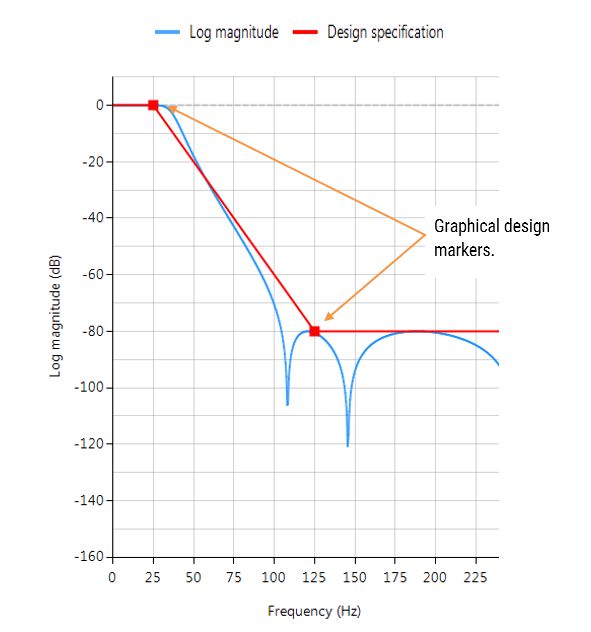
Der ASN Filter Designer bietet Ingenieuren eine einfach zu bedienende, intuitive grafische Design-Entwicklungsplattform für den Entwurf von digitalen IIR- und FIR-Filtern. Das Echtzeit-Entwurfsparadigma des Tools nutzt grafische Entwurfsmarker, die es dem Designer ermöglichen, seine Anforderungen an den Größen-Frequenzgang in Echtzeit einfach zu zeichnen und zu modifizieren, während das Tool automatisch die exakten Spezifikationen für sie ausfüllt.
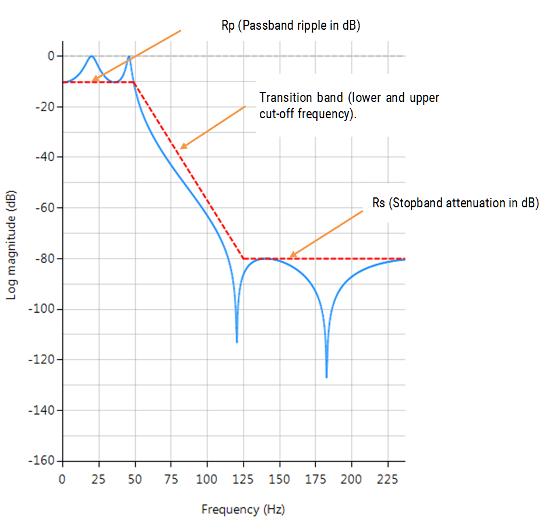
Betrachten Sie den Entwurf der folgenden technischen Spezifikation:
| Fs: | 500Hz |
| Durchlassband-Frequenz: | 0-40Hz |
| Typ: | Tiefpass |
| Verfahren: | Elliptisch |
| Sperrbanddämpfung @ 125Hz: | ≥ 80 dB |
| Passband ripple: | < 0.1dB |
| Ordnung | Klein wie möglich |
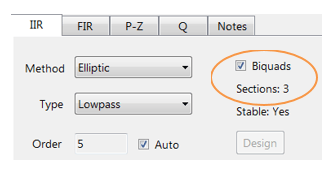
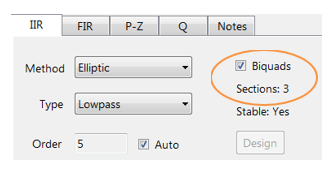
Durch die grafische Eingabe der Spezifikationen in den ASN Filter Designer und die Feinabstimmung der Positionen der Entwurfsmarker entwirft das Tool das Filter automatisch als Biquad-Kaskade (diese Terminologie wird in den folgenden Abschnitten erläutert), wählt automatisch die erforderliche Filterordnung und erzeugt im Wesentlichen automatisch die genaue technische Spezifikation des Filters!
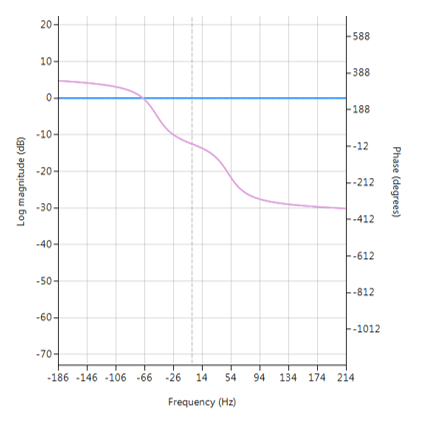
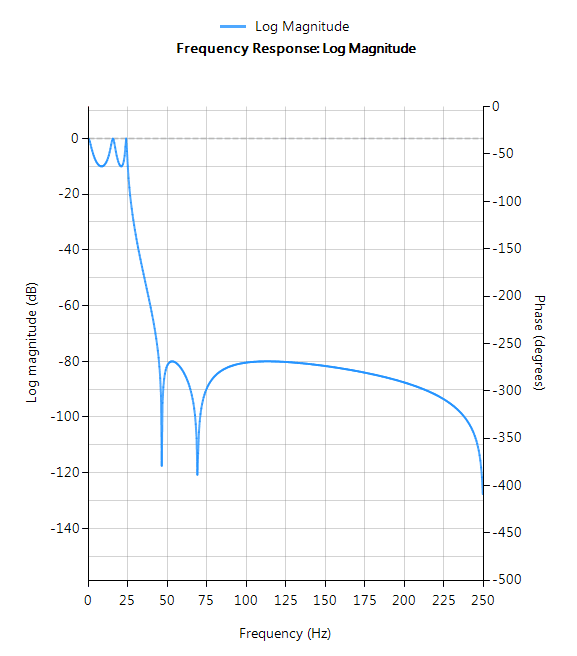
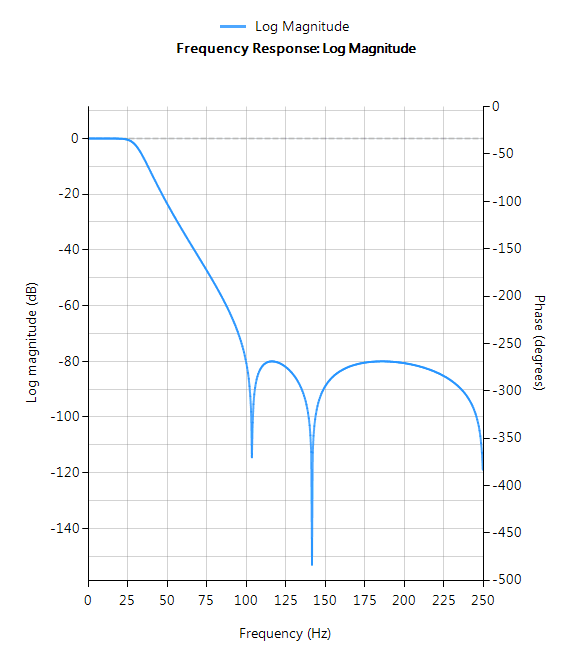
Der Frequenzgang eines elliptischen IIR-Tiefpassfilters 5. Ordnung, der die Spezifikationen erfüllt, ist unten dargestellt:
Dieses Tiefpaßfilter 5. Ordnung bildet die Grundlage für die hier geführte Diskussion.
Biquad-IIR-Filter
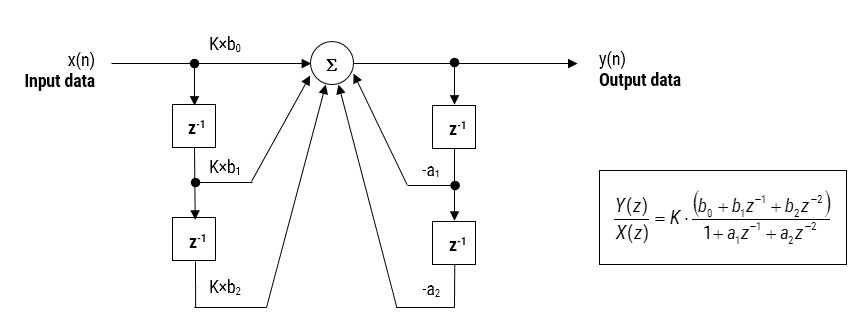
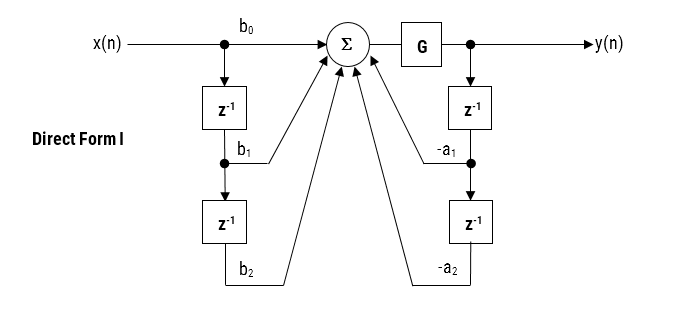
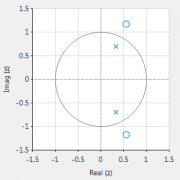
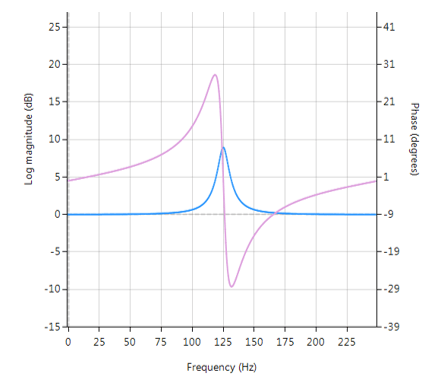
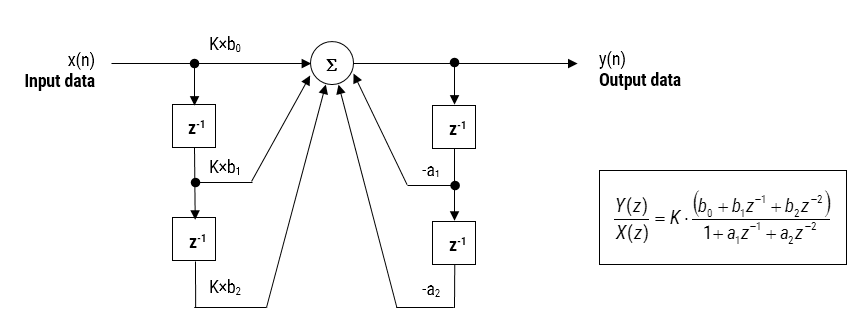
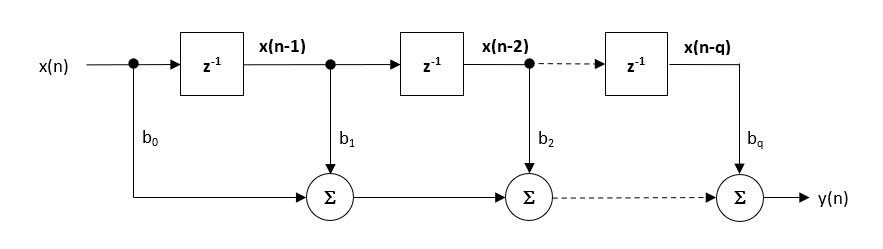
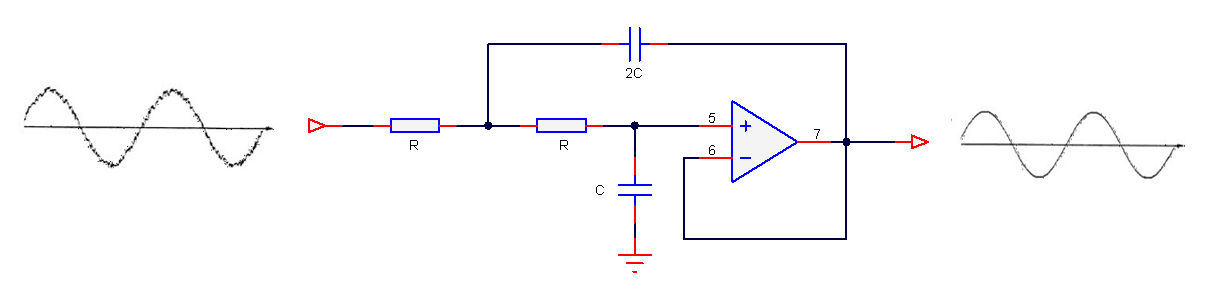
Die hier besprochene IIR-Filter-Implementierung wird als Biquad bezeichnet, da sie zwei Pole und zwei Nullstellen hat, wie in Abbildung 1 dargestellt. Die Biquad-Implementierung ist besonders nützlich für Festkomma-Implementierungen, da die Auswirkungen der Quantisierung und der numerischen Stabilität minimiert werden. Der Gesamterfolg jeder Biquad-Implementierung hängt jedoch von der verfügbaren Zahlengenauigkeit ab, die ausreichend sein muss, um sicherzustellen, dass die quantisierten Pole immer innerhalb des Einheitskreises liegen.
Abbildung 1: Direkte Form I (Biquad) IIR-Filterrealisierung und Übertragungsfunktion
Bei der Analyse von Abbildung 1 ist zu erkennen, dass die Biquad-Struktur eigentlich aus zwei Rückkopplungspfaden (skaliert mit \(a_1\) und \(a_2\)), drei Vorwärtspfaden (skaliert mit \(b_0, b_1\) und \(b_2\)) und einer Abschnittsverstärkung \(K\) besteht. Somit kann die Filterfunktion von Abbildung 1 durch die folgende einfache rekursive Gleichung zusammengefasst werden:
\(\displaystyle y(n)=K\times\Big[b_0 x(n) + b_1 x(n-1) + b_2 x(n-2)\Big] – a_1 y(n-1)-a_2 y(n-2)\)
Bei der Analyse der Gleichung fällt auf, dass die Biquad-Implementierung nur vier Additionen (die nur einen Akkumulator benötigen) und fünf Multiplikationen erfordert, was auf jedem Cortex-M-Mikrocontroller leicht untergebracht werden kann. Die Abschnittsverstärkung K kann auch vor der Implementierung mit den Vorwärtswegkoeffizienten vormultipliziert werden.
Eine Sammlung von Biquad-Filtern wird als Biquad-Kaskade bezeichnet, wie unten dargestellt.
Der ASN Filter Designer kann eine Kaskade von bis zu 50 Biquads entwerfen und implementieren (nur Professional Edition).
Fließkomma-Implementierung
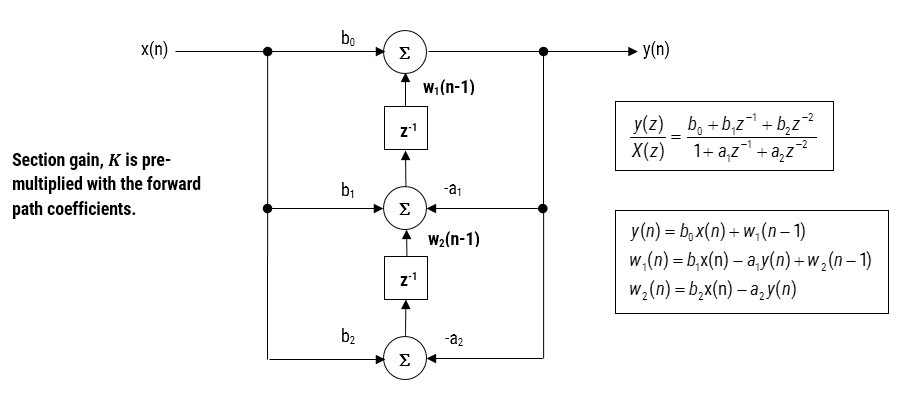
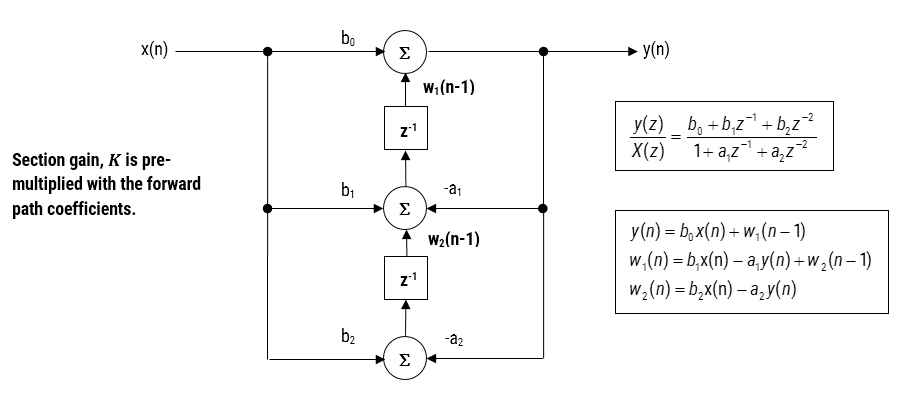
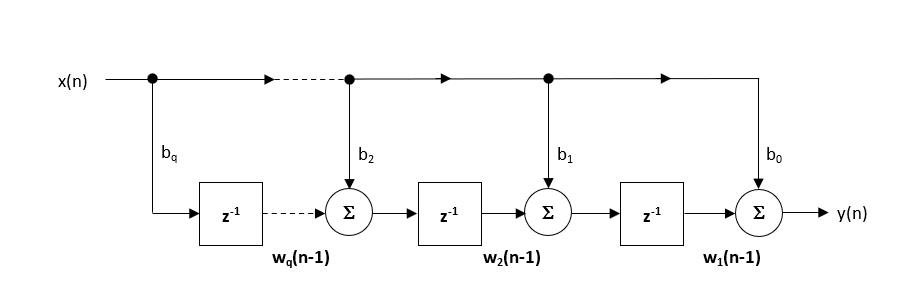
Bei der Implementierung eines Filters in Fließkomma (d. h. unter Verwendung von Arithmetik mit doppelter oder einfacher Genauigkeit) gelten Direct Form II-Strukturen als bessere Wahl als die Direct Form I-Struktur. Die Direct Form II Transposed-Struktur gilt als die numerisch genaueste für die Fließkomma-Implementierung, da die unerwünschten Effekte der numerischen Übersättigung minimiert werden, wie bei der Analyse der Differenzgleichungen zu sehen ist.
Abbildung 2 – Direct Form II Transposed-Struktur, Übertragungsfunktion und Differenzengleichungen
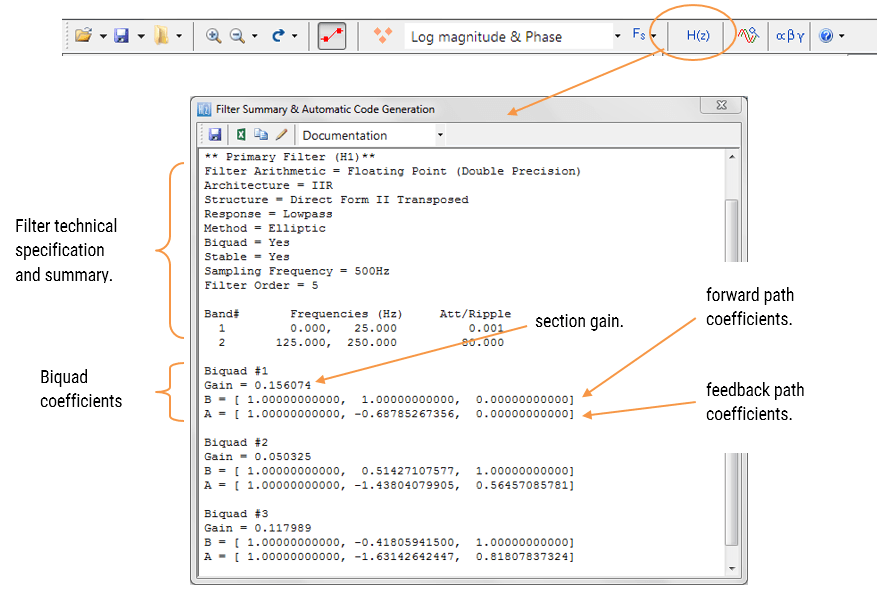
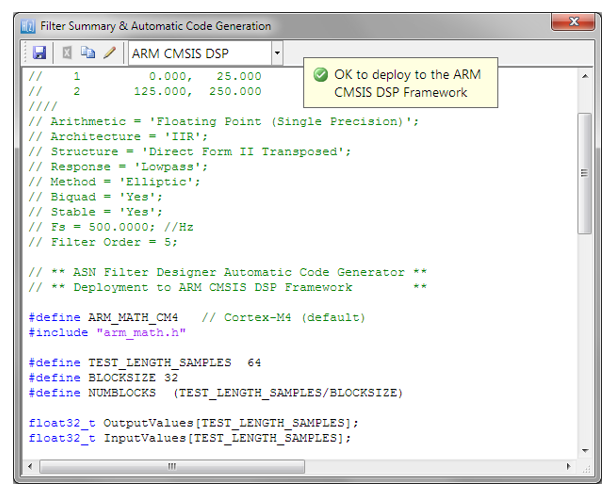
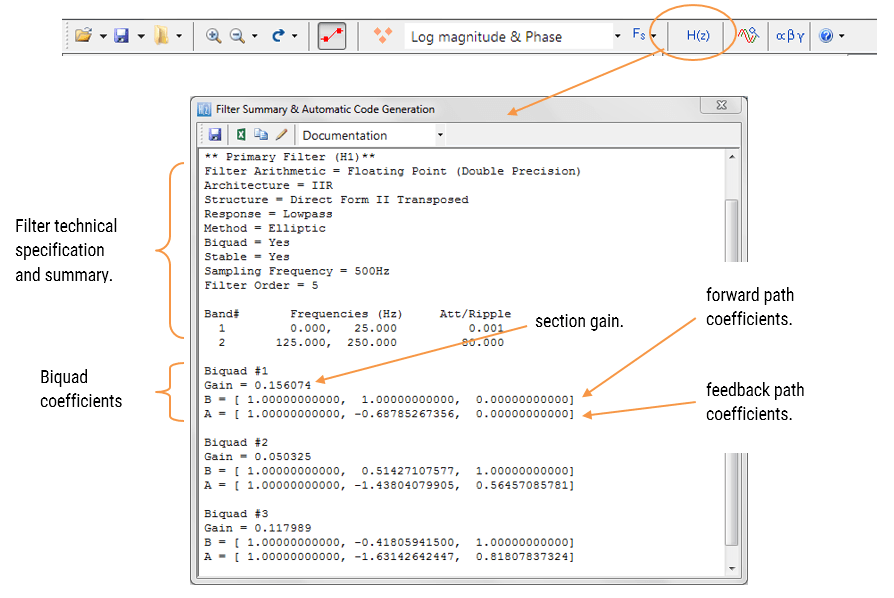
Die Filter Zusammenfassung (siehe Abbildung 3) bietet dem Designer einen detaillierten Überblick über das entworfene Filter, einschließlich einer ausführlichen Zusammenfassung der technischen Spezifikationen und der Filterkoeffizienten, was einen schnellen und einfachen Weg zur Dokumentation Ihres Entwurfs darstellt.
Der ASN Filter Designer unterstützt den Entwurf und die Implementierung sowohl von Single Section als auch von Biquad (Standardeinstellung) IIR-Filtern. Da das CMSIS-DSP-Framework jedoch keine direkte Unterstützung für Single Section IIR-Filter bietet, wird diese Funktion in dieser Application Note nicht behandelt.

Die Implementierung des CMSIS-DSP-Software-Frameworks erfordert die Vorzeicheninversion (d. h. das Umkehren des Vorzeichens) der Rückkopplungskoeffizienten. Um dies zu ermöglichen, kehrt die automatische Code-Generierungs-Engine des Tools das Vorzeichen der Rückkopplungskoeffizienten bei Bedarf automatisch um. In diesem Fall wird der Satz von Differenzgleichungen zu,
\(y(n)=b_0 x(n)+w_1 (n-1)\)
\(w_1 (n)= b_1 x(n)+a_1 y(n)+w_2 (n-1)\)
\(w_2 (n)= b_2 x(n)+a_2 y(n)\)
Abbildung 3: ASN Filter Designer: Filterzusammenfassung
Automatische Code-Generierung für Arm-Prozessorkerne über CMSIS-DSP
Die automatische Code-Generierungs-Engine des ASN Filter Designers erleichtert den Export eines entworfenen Filters auf Cortex-M Arm-basierte Prozessoren über das CMSIS-DSP Software-Framework. Die integrierten Analyse- und Hilfefunktionen des Tools unterstützen den Designer bei der erfolgreichen Konfiguration des Designs für den Einsatz.
Alle Entwürfe von Fließkomma-IIR-Filtern müssen auf Single-Precision-Arithmetik und entweder auf einer Direct Form I oder Direct Form II Transposed-Filterstruktur basieren. Wie im vorherigen Abschnitt beschrieben, wird die Direct Form II Transposed-Struktur aufgrund ihrer höheren numerischen Genauigkeit für die Fließkomma-Implementierung befürwortet.
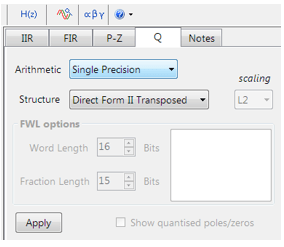
Die Einstellungen für Quantisierung und Filterstruktur finden Sie unter der Registerkarte Q (wie links dargestellt). Durch Einstellen von Arithmetic auf Single Precision und Structure auf Direct Form II Transposed und Klicken auf die Schaltfläche Apply wird die hier betrachtete IIR für das Software-Framework CMSIS-DSP konfiguriert.
Wählen Sie das Arm CMSIS-DSP-Framework aus der Auswahlbox im Filterübersichtsfenster aus:
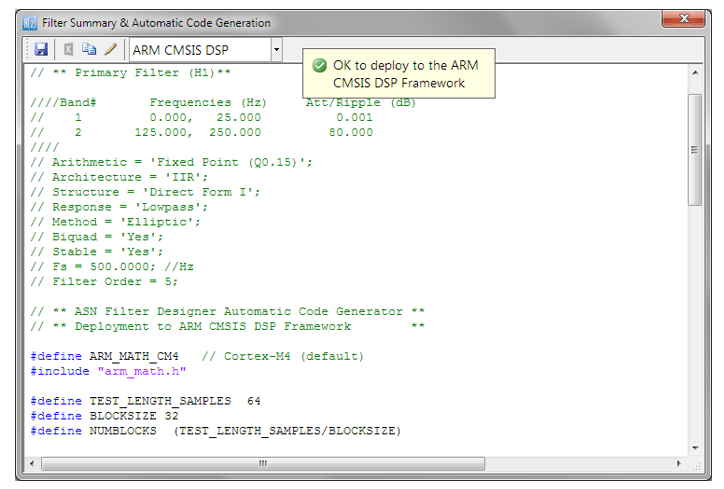
Der automatisch generierte C-Code auf Basis des CMSIS-DSP-Frameworks für die direkte Implementierung auf einem Arm-basierten Cortex-M-Prozessor ist unten dargestellt:
Wie man sieht, generiert der automatische Code-Generator den gesamten Initialisierungscode, die Skalierung und die Datenstrukturen, die für die Implementierung des IIR über die CMSIS-DSP-Bibliothek benötigt werden. Dieser Code kann direkt in jedem Cortex-M-basierten Entwicklungsprojekt verwendet werden – ein vollständiges Keil-MDK-Beispiel ist auf der Website von Arm/Keil verfügbar. Beachten Sie, dass der Code-Generator des Werkzeugs standardmäßig Code für den Cortex-M4-Kern erzeugt. Bitte entnehmen Sie der folgenden Tabelle die #define-Definition, die für alle unterstützten Kerne erforderlich ist.
ARM_MATH_CM0 | Cortex-M0 core. | ARM_MATH_CM4 | Cortex-M4 core. |
ARM_MATH_CM0PLUS | Cortex-M0+ core. | ARM_MATH_CM7 | Cortex-M7 core. |
ARM_MATH_CM3 | Cortex-M3 core. | ||
ARM_MATH_ARMV8MBL | ARMv8M Baseline target (Cortex-M23 core). | ||
ARM_MATH_ARMV8MML | ARMv8M Mainline target (Cortex-M33 core). |

Die automatische Code-Generierung von IIR-Filtern mit komplexen Koeffizienten wird derzeit nicht unterstützt.
Implementieren des Filters im Arm Keil’s MDK
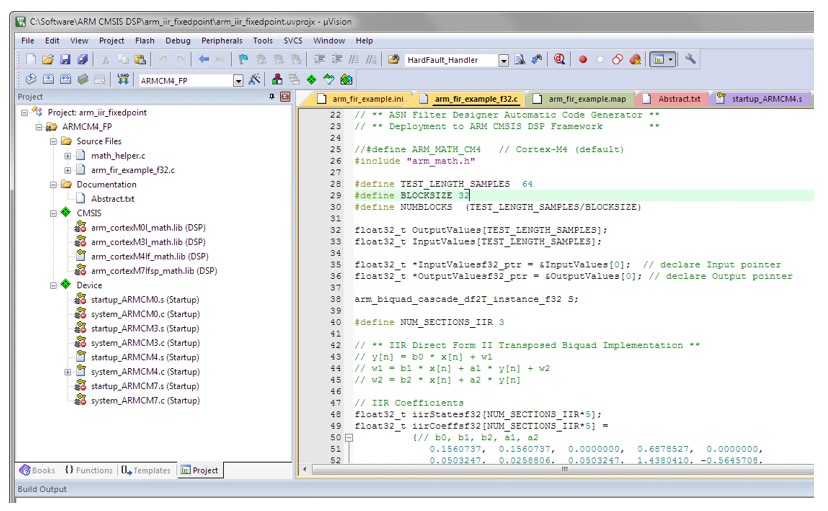
Wie im vorherigen Abschnitt erwähnt, kann der vom Arm CMSIS-DSP Code-Generator erzeugte Code direkt in jedem Cortex-M-basierten Entwicklungsprojekt-Tooling verwendet werden, wie z. B. Arm Keils Industriestandard μVision MDK (Mikrocontroller-Entwicklungskit).
Ein komplettes μVision-Beispiel-IIR-Biquad-Filterprojekt kann von Keils Website heruntergeladen werden und ist, wie unten zu sehen, so einfach wie das Kopieren und Einfügen des Codes und das Vornehmen kleiner Anpassungen am Code.
Das Beispielprojekt nutzt die leistungsstarken Simulationsmöglichkeiten von μVision und ermöglicht die Evaluierung des IIR-Filters auf M0-, M3-, M4- bzw. M7-Cores. Als zusätzlicher Bonus kann auch der Logik-Analysator von μVision verwendet werden, so dass Vergleiche zwischen dem Signal-Analysator des ASN Filter Designers und der Realität auf einem Cortex-M-Kern möglich sind.
Festkomma-Implementierung
Wie bereits erwähnt, ist die direkte Form I-Filterstruktur die beste Wahl für die Festkomma-Implementierung. Vor der Implementierung der Differenzgleichung auf einem Festkommaprozessor müssen jedoch einige wichtige Überlegungen zur Datenskalierung berücksichtigt werden. Da das CMSIS-DSP-Framework nur die Datentypen Q15 und Q31 für IIR-Filter unterstützt, bezieht sich die folgende Diskussion auf eine Implementierung auf einer 16-Bit-Wort-Architektur, d. h. auf Q15.
Quantisierung
Um die Koeffizienten und Ein-/Ausgangszahlen korrekt darzustellen, wird die Systemwortlänge (16 Bit für die Zwecke dieser Application Note) zunächst in ihre Anzahl an Ganzzahlen und Nachkommastellen aufgeteilt. Das allgemeine Format ist gegeben durch:
Q Num of Integers.Fraction length
Wenn wir annehmen, dass alle Datenwerte innerhalb eines Maximal-/Minimalbereichs von \(\pm 1\) liegen, können wir das Format Q0.15 verwenden, um alle Zahlen entsprechend darzustellen. Beachten Sie, dass das Q0.15-Format (oder einfach Q15) ein Maximum von \(\displaystyle 1-2^{-15}=0.9999=0x7FFF\) und ein Minimum von \(-1=0x8000\) (Zweierkomplement-Format) darstellt.
Der ASN Filter Designer kann für die Festkomma-Q15-Arithmetik konfiguriert werden, indem die Spezifikationen für die Wortlänge und die Fraktale Länge in der Registerkarte Q eingestellt werden (siehe Abschnitt Konfiguration für die Details). Ein offensichtliches Problem, das sich bei Biquads zeigt, ist jedoch der Zahlenbereich der Koeffizienten. Da Pole überall innerhalb des Einheitskreises platziert werden können, wird das resultierende Polynom, das für die Implementierung benötigt wird, oft im Bereich \(\pm 2\) liegen, was eine Q14-Arithmetik erfordern würde. Um dieses Problem zu umgehen, werden alle Zähler- und Nennerkoeffizienten über einen biquadischen Post-Scaling-Faktor skaliert, wie unten beschrieben.
Post-Scaling-Faktor
Um sicherzustellen, dass die Koeffizienten in die Spezifikationen für die Wortlänge und die fraktionale Länge passen, enthalten alle IIR-Filter einen Post-Scaling-Faktor, der die Zähler- und Nennerkoeffizienten entsprechend skaliert. Als Folge dieser Skalierung muss der Post-Scaling-Faktor in die Filterstruktur einbezogen werden, um einen korrekten Betrieb zu gewährleisten.
Das Konzept der Post-Scaling wird im Folgenden für eine Biquad-Implementierung der direkten Form I dargestellt.
Abbildung 4: Direkte Form I-Struktur mit Post-Scaling
Durch Vormultiplikation der Zählerkoeffizienten mit der Querschnittsverstärkung \(K\) kann nun jeder Koeffizient mit \(G\) skaliert werden, d. h. \(\displaystyle b_0=\frac{b_0}{G}, b_1=\frac{b_1}{G}, a_1=\frac{a_1}{G}, a_2=\frac{a_2}{G}\) usw. Daraus ergibt sich nun die folgende Differenzengleichung:
\(\displaystyle y(n)=G \times\Big [b_0 x(n) + b_1 x(n-1) + b_2 x(n-2) – a_1 y(n-1)-a_2 y(n-2)\Big]\)

Alle im Tool implementierten IIR-Strukturen beinhalten das Konzept des Post-Scaling-Faktors. Diese Skalierung ist für die Implementierung über das Arm CMSIS-DSP-Framework obligatorisch – weitere Details finden Sie im Abschnitt “Konfiguration”.
Verstehen der Filterzusammenfassung
Um die in der ASN Filter Designer Filterzusammenfassung dargestellten Informationen vollständig zu verstehen, zeigt das folgende Beispiel die Filterkoeffizienten, die mit Double Precision Arithmetik und mit Fixed Point Q15 Quantisierung erhalten wurden.
Anwendung der Festkomma-Q15-Arithmetik (beachten Sie die Auswirkungen der Quantisierung auf die Koeffizientenwerte):
Konfigurieren des ASN Filter Designers für Festkomma-Arithmetik
Um ein IIR-Fixed-Point-Filter über das CMSIS-DSP-Framework zu implementieren, müssen alle Designs auf der Fixed-Point-Arithmetik (entweder Q15 oder Q31) und der Direct-Form-I-Filterstruktur basieren.
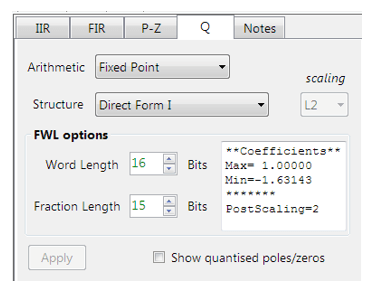
Die Einstellungen für Quantisierung und Filterstruktur finden Sie unter der Registerkarte Q (wie links dargestellt): Wenn Sie Arithmetic auf Fixed Point und Structure auf Direct Form I einstellen und auf die Schaltfläche Apply klicken, wird die hier betrachtete IIR für das CMSIS-DSP-Software-Framework konfiguriert.

Der Post-Scaling-Faktor ist im CMSIS-DSP-Software-Framework tatsächlich als \( \log_2 G\) implementiert (d. h. eine nach links verschobene Skalierungsoperation, wie in Abbildung 4 dargestellt).

Eingebaute Analytik: Das Tool analysiert automatisch die Filterkoeffizienten der Kaskade und wählt einen geeigneten Skalierungsfaktor. Wie oben zu sehen, ist der größte Minimalwert -1,63143, daher ist ein Post-Scaling-Faktor von 2 erforderlich, um alle Koeffizienten in die Q15-Arithmetik “einzupassen”.
Vergleich von Spektren, die durch unterschiedliche Rechenregeln erhalten wurden
Um die Übersichtlichkeit und die allgemeine Berechnungsgeschwindigkeit zu verbessern, zeigt der ASN Filter Designer nur Spektren (d.h. Magnitude, Phase usw.) an, die auf den aktuellen arithmetischen Regeln basieren. Dies ist etwas anders als bei anderen Werkzeugen, die Multispektren anzeigen, die durch (z. B.) Festkomma– und Doppelpräzisionsarithmetik erhalten wurden. Für alle Benutzer, die Spektren vergleichen möchten, können Sie einfach zwischen den arithmetischen Einstellungen wechseln, indem Sie die Arithmetic methode ändern. Der Designer berechnet dann automatisch die Filterkoeffizienten unter Verwendung der gewählten Rechenregeln und der aktuellen technischen Spezifikation neu. Das Diagramm wird dann unter Verwendung der aktuellen Zoom-Einstellungen aktualisiert.
Automatische Code-Generierung für das Arm CMSIS-DSP-Framework
Wie bei der Fließkomma-Arithmetik wählen Sie das Arm CMSIS-DSP-Framework aus der Auswahlbox im Filter-Übersichtsfenster aus:
Der automatisch generierte C-Code auf Basis des CMSIS-DSP-Frameworks für die direkte Implementierung auf einem Arm-basierten Cortex-M-Prozessor ist unten dargestellt:
Wie beim Fließkommafilter generiert der automatische Code-Generator den gesamten Initialisierungscode, die Skalierung und die Datenstrukturen, die zur Implementierung des IIR über die CMSIS-DSP-Bibliothek benötigt werden. Dieser Code kann direkt in jedem Cortex-M-basierten Entwicklungsprojekt verwendet werden – ein vollständiges Keil-MDK-Beispiel ist auf der Website von Arm/Keil verfügbar. Beachten Sie, dass der Code-Generator des Werkzeugs standardmäßig Code für den Cortex-M4-Kern erzeugt. Bitte entnehmen Sie der folgenden Tabelle die #define -Definition, die für alle unterstützten Kerne erforderlich ist.
ARM_MATH_CM0 | Cortex-M0 core. | ARM_MATH_CM4 | Cortex-M4 core. |
ARM_MATH_CM0PLUS | Cortex-M0+ core. | ARM_MATH_CM7 | Cortex-M7 core. |
ARM_MATH_CM3 | Cortex-M3 core. | ||
ARM_MATH_ARMV8MBL | ARMv8M Baseline target (Cortex-M23 core). | ||
ARM_MATH_ARMV8MML | ARMv8M Mainline target (Cortex-M33 core). |
Der Hauptcode der Testschleife (nicht gezeigt) dreht sich um die Funktion arm_biquad_cascade_df2T_f32(), die die Filterung eines Blocks von Eingangsdaten durchführt.

IIR-Filter mit komplexen Koeffizienten werden derzeit nicht unterstützt.
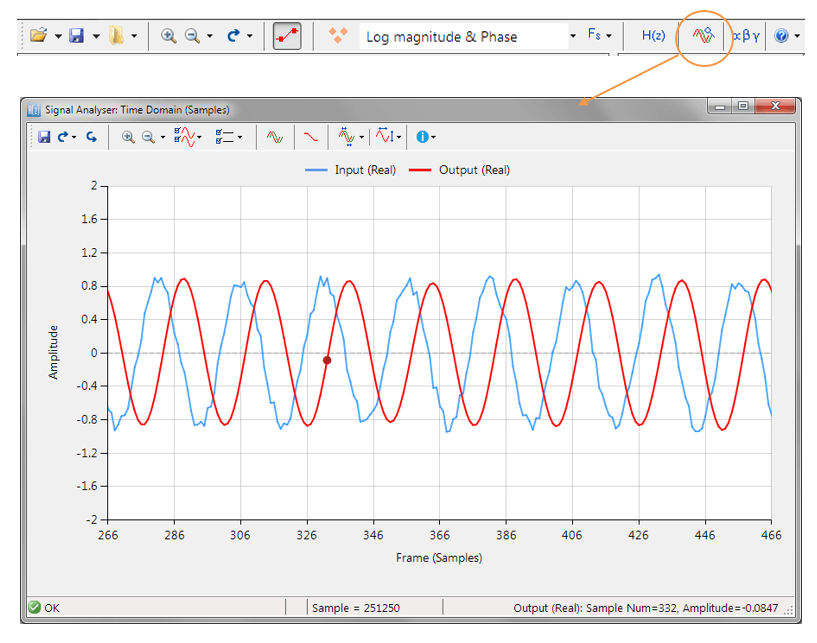
Validierung des Entwurfs mit dem Signal Analyser
Ein Entwurf kann mit dem Signal Analyser validiert werden, wobei sowohl Zeit- als auch Frequenzbereichsdiagramme unterstützt werden. Ein umfassender Signalgenerator ist vollständig in den Signalanalysator integriert, so dass die Entwickler ihre Filter mit einer Vielzahl von Eingangssignalen testen können, wie z. B. Sinuswellen, weißes Rauschen oder sogar externe Testdaten.
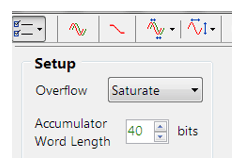
Für Festkomma-Implementierungen erlaubt das Tool den Entwicklern, die Overflow-Arithmetikregeln als: Saturate oder Wrap. Außerdem kann die Accumulator Word Length zwischen 16 und 40 Bit eingestellt werden, so dass die Entwickler schnell die optimalen Einstellungen für ihre Anwendung finden können.
Zusätzliche Ressourcen
- Digital signal processing: principles, algorithms and applications, J.Proakis and D.Manoloakis
- Digital signal processing: a practical approach, E.Ifeachor and B.Jervis.
- Digital filters and signal processing, L.Jackson.
- Step by step video tutorial of designing an IIR and deploying it to Keil MDK uVision.
- Implementing Biquad IIR filters with the ASN Filter Designer and the Arm CMSIS-DSP software framework (ASN-AN025)
- Keil MDK uVision example IIR filter project