Moderne eingebettete Prozessoren, Software-Frameworks und Design-Tools ermöglichen es Ingenieuren jetzt, im Rahmen der I4.0-Revolution fortschrittliche Messkonzepte in intelligenten Fabriken anzuwenden.

In den letzten Jahren hat die vorausschauende Wartung (Predictive Maintenance) von Maschinen große Beachtung gefunden, da Fabriken ihre Produktionseffizienz maximieren und gleichzeitig die unschätzbaren Fähigkeiten erfahrener Vorarbeiter und Produktionsmitarbeiter erhalten wollen.
Früher ging ein Vorarbeiter durch die Werkshalle und hörte auf die Geräusche, die eine Maschine machte, um eine Vorstellung von einem bevorstehenden Ausfall zu bekommen. Mit dem Aufkommen der I4.0-Technologie können nun Mikrofone, DSP-Algorithmen und ML eingesetzt werden, um den Geräuschen einer Maschine zuzuhören” und dann eine Klassifizierung und Vorhersage zu treffen.
Eine der größten Herausforderungen ist die Frage, wie man einen Computer dazu bringt, wie ein Mensch zu hören.
Die Physik des menschlichen Ohrs
Rechts ist eine Abbildung des menschlichen Ohrs zu sehen. Wie man sieht, besteht die grundlegende Aufgabe des Ohrs darin, Schall (Luftschwingungen) in elektrische Nervenimpulse umzuwandeln, die vom Gehirn interpretiert werden.
Eine Illustration des menschlichen Ohrs auf der rechten Seite. Wie man sieht, besteht die grundlegende Aufgabe des Ohrs darin, Schall (Luftschwingungen) in elektrische Nervenimpulse zu übersetzen, die vom Gehirn interpretiert werden.
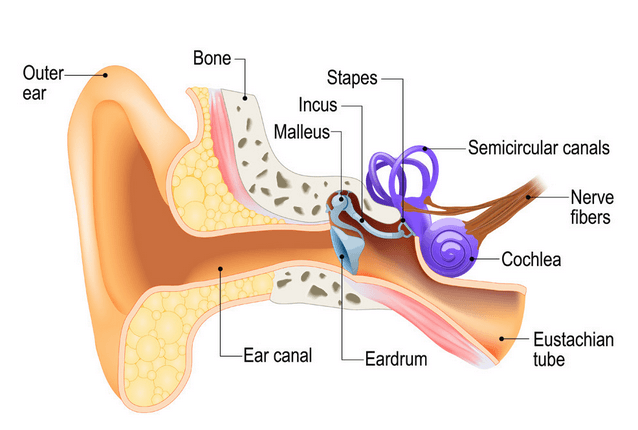
Wie funktioniert das?
Das Ohr erreicht dies über drei Knochen (Stapes, Incus und Malleus), die als mechanische Verstärker für die am Trommelfell empfangenen Schwingungen fungieren. Diese verstärkten Töne werden dann über das ovale Fenster (nicht abgebildet) an die Cochlea weitergeleitet. Die Cochlea (lila dargestellt) ist mit einer Flüssigkeit gefüllt, die sich als Reaktion auf die Schwingungen des ovalen Fensters bewegt. Während sich die Flüssigkeit bewegt, werden Tausende von Nervenenden in Bewegung gesetzt. Diese Nervenenden wandeln die Schallschwingungen in elektrische Impulse um, die entlang der Hörnervenfasern zum Gehirn geleitet und dort ausgewertet werden.
Modellierung des wahrgenommenen Schalls
Aufgrund der Komplexität des strömungsmechanischen Aufbaus des menschlichen Gehörs sind tiefe und hohe Frequenzen normalerweise nicht wahrnehmbar. Forscher haben im Laufe der Jahre herausgefunden, dass der Mensch Geräusche im Bereich von 1-6 kHz am besten wahrnimmt, wobei dieser Bereich je nach dem Gesundheitszustand der Person variiert.
Diese Forschung führte zur Definition einer Reihe von Bewertungskurven: die sogenannten A-, B-, C- und D-Bewertungskurven, die den Frequenzgang eines Mikrofons ausgleichen. Diese Gewichtungskurven zielen darauf ab, die digitale und die physische Welt einander anzunähern, indem sie es einem computergestützten Mikrofonsystem ermöglichen, wie ein Mensch zu hören.
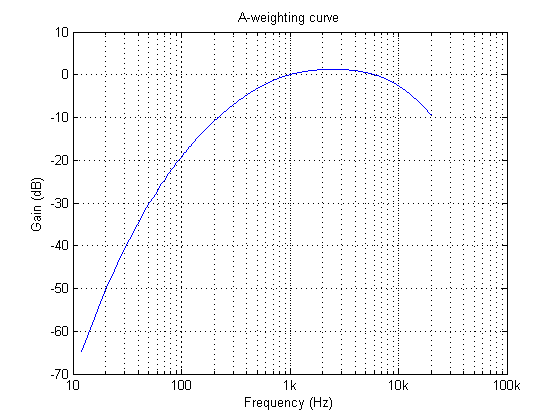
Die A-Bewertungskurve ist die am weitesten verbreitete Kurve, da sie gemäß IEC-61672 in allen Schallpegelmessern enthalten sein muss. Die B- und D-Kurven werden kaum verwendet, aber die C-Bewertung kann zur Prüfung der Auswirkungen von Lärm in Telekommunikationssystemen eingesetzt werden.
Der Frequenzgang der A-Bewertungskurve ist oben abgebildet. Es ist zu erkennen, dass Geräusche, die in unser Ohr eindringen, unterhalb von 500 Hz unterdrückt werden und zwischen 0,5 und 6 kHz am stärksten wahrnehmbar sind. Beachten Sie, dass die Kurve oberhalb von 20kHz nicht spezifiziert ist, da dies den menschlichen Hörbereich überschreitet.
ASN FilterScript
Die symbolische mathematische Skriptsprache FilterScript von ASN bietet Entwicklern die Möglichkeit, eine analoge Filterübertragungsfunktion mit nur wenigen Zeilen Code in ihr digitales Äquivalent umzuwandeln.
Die analogen Übertragungsfunktionen der A- und C-Bewertungskurven sind unten angegeben:
\(H_A(s) \approx \displaystyle{7.39705×10^9 \cdot s^4 \over (s + 129.4)^2\quad(s + 676.7)\quad (s + 4636)\quad (s + 76655)^2}\)
\(H_C(s) \approx \displaystyle{5.91797×10^9 \cdot s^2\over(s + 129.4)^2\quad (s + 76655)^2}\)
Diese analogen Übertragungsfunktionen können mit Hilfe der Funktion bilinear() in ihre digitalen Äquivalente umgewandelt werden. Es ist jedoch zu beachten, dass \(H_A(s) \) ein erhebliches Maß an algebraischer Manipulation erfordert, um die Koeffizienten des Nenners in Potenzen von \(s\) zu extrahieren.
Faltung
Ein einfacher Trick für die Multiplikation von Polynomen ist die lineare Faltung, die dieselbe algebraische Operation ist wie die Multiplikation von zwei Polynomen miteinander. Dies lässt sich leicht mit der Funktion conv() von Filterscript wie folgt durchführen:
y=conv(a,b);
Als einfaches Beispiel würde die Multiplikation von \((s^2+2s+10)\) mit \((s+5)\) durch die folgenden drei Zeilen FilterScript-Code definiert:
a={1,2,10};
b={1,5};
y=conv(a,b);
which yields, 1 7 20 50 or \((s^3+7s^2+20s+50)\)
Für die Laplace-Übertragungsfunktion der A-Bewertungskurve ist der vollständige FilterScript-Code unten angegeben:
ClearH1; // clear primary filter from cascade
Main() // main loop
a={1, 129.4};
b={1, 676.7};
c={1, 4636};
d={1, 76655};
aa=conv(a,a); // polynomial multiplication
dd=conv(d,d);
aab=conv(aa,b);
aabc=conv(aab,c);
Na=conv(aabc,dd);
Nb = {0 ,0 , 1 ,0 ,0 , 0, 0}; // define numerator coefficients
G = 7.397e+09; // define gain
Ha = analogtf(Nb, Na, G, "symbolic");
Hd = bilinear(Ha,0, "symbolic");
Num = getnum(Hd);
Den = getden(Hd);
Gain = getgain(Hd)/computegain(Hd,1e3); // set gain to 0dB@1kHz
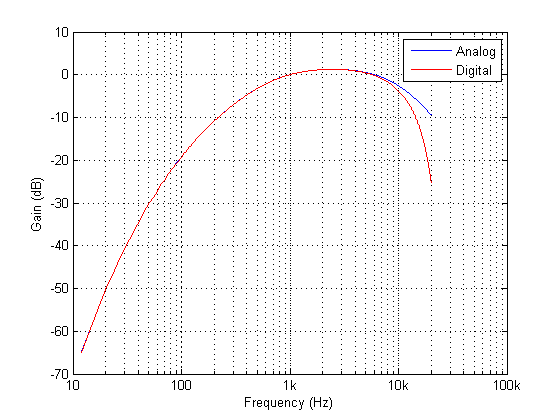
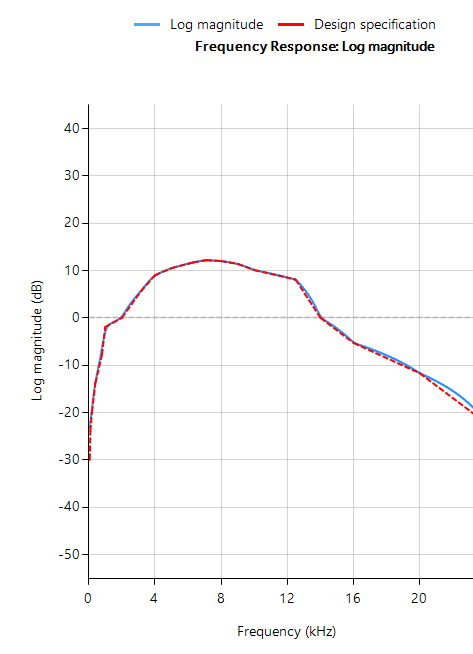
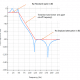
Frequenzgang des analogen gegenüber dem digitalen A-Bewertungsfilter für \(f_s=48kHz\). Wie zu sehen ist, stimmt der digitale äquivalente Amplitudengang bis \(6kHz\) sehr gut mit dem idealen analogen Amplitudengang überein.
Die ITU-R 486-4-Bewertungskurve
Eine weitere interessante Bewertungskurve ist die von der BBC entwickelte ITU-R 486-4-Bewertungskurve. Im Gegensatz zum A-Bewertungsfilter beschreibt die ITU-R 468-4-Kurve die subjektive Lautheit für breitbandige Reize. Der Hauptnachteil der A-Bewertungskurve besteht darin, dass sie die Lautheitsbeurteilung realer Reize insbesondere im Frequenzband von etwa 1-9 kHz unterschätzt.
Aufgrund der genauen Definition der 486-4-Bewertungskurve ist keine analoge Übertragungsfunktion verfügbar. Stattdessen liefert die Norm eine Tabelle mit Amplituden und Frequenzen – siehe hier. Diese Spezifikation kann direkt in die firarb() -Funktion von Filterscript eingegeben werden, um ein geeignetes FIR-Filter zu entwerfen, wie unten gezeigt:
ClearH1; // clear primary filter from cascade
ShowH2DM;
interface L = {10,400,10,250}; // filter order
Main()
// ITU-R 468 Weighting
A={-29.9,-23.9,-19.8,-13.8,-7.8,-1.9,0,5.6,9,10.5,11.7,12.2,12,11.4,10.1,8.1,0,-5.3,-11.7,-22.2};
F={63,100,200,400,800,1e3,2e3,3.15e3,4e3,5e3,6.3e3,7.1e3,8e3,9e3,1e4,1.25e4,1.4e4,1.6e4,2e4};
A={-30,A}; // specify arb response
F={0,F,fs/2}; //
Hd=firarb(L,A,F,"blackman","numeric");
Num=getnum(Hd);
Den={1};
Gain=getgain(Hd);
Frequenzgang eines ITU-R 468-4 FIR-Filters, der mit der firarb()-Funktion von Filterscript für \(f_s=48kHz\) entworfen wurde.
Wie Sie gesehen haben, bietet FilterScript dem Designer eine sehr leistungsfähige symbolische Skriptsprache für den Entwurf von Gewichtungskurvenfiltern. Die folgende Diskussion konzentriert sich nun auf die Implementierung des A-Bewertungsfilters auf einem Arm-basierten Prozessor über den automatischen Codegenerator des Tools. Die im Folgenden vorgestellten Konzepte und Schritte gelten gleichermaßen für FIR-Filter.
Automatische Codegenerierung für Arm-Prozessorkerne über CMSIS-DSP
Die automatische Codegenerierung des ASN Filter Designers erleichtert den Export eines entworfenen Filters auf Cortex-M Arm basierte Prozessoren über das CMSIS-DSP Software Framework. Die integrierten Analyse- und Hilfefunktionen des Tools unterstützen den Designer bei der erfolgreichen Konfiguration des Designs für den Einsatz.
Vor der Generierung des Codes muss der H2-Filter (d. h. der in FilterScript entworfene Filter) zunächst für den Einsatz in eine H1-Filterstruktur (Hauptfilter) umoptimiert (transformiert) werden. Das Options Menü befindet sich unter der Registerkarte P-Z in der Hauptbenutzeroberfläche.
Alle Entwürfe von Fließkomma-IIR-Filtern müssen auf Single-Precision-Arithmetik und entweder auf einer Direct Form I– oder Direct Form II Transposed -Filterstruktur basieren. Die Struktur Direct Form II Transposed wird für die Fließkomma-Implementierung empfohlen, da sie eine höhere numerische Genauigkeit aufweist.
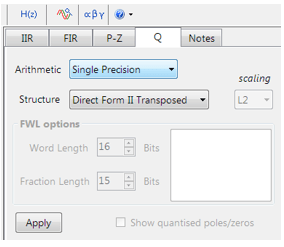
Die Einstellungen für die Quantisierung und die Filterstruktur finden Sie auf der Registerkarte Q (wie links dargestellt). Wenn Sie die Arithmetic auf Single Precision und Structure auf Direct Form II Transposed einstellen und auf die Schaltfläche Apply klicken, wird die hier betrachtete IIR für das CMSIS-DSP Software Framework konfiguriert.
Wählen Sie das Arm CMSIS-DSP-Framework aus der Auswahlbox im Filterübersichtsfenster:
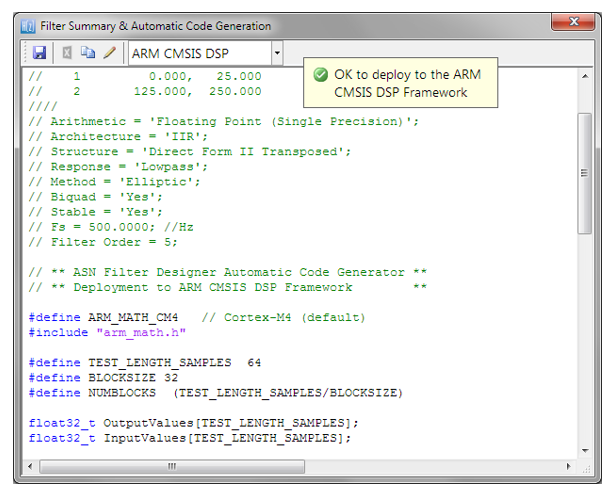
Der automatisch generierte C-Code auf Basis des CMSIS-DSP-Frameworks für die direkte Implementierung auf einem Arm-basierten Cortex-M-Prozessor ist unten dargestellt:
Wie man sieht, generiert der automatische Code-Generator des ASN Filter Designers den gesamten Initialisierungscode, die Skalierung und die Datenstrukturen, die für die Implementierung des IIR-Filters mit A-Bewertung über die CMSIS-DSP-Bibliothek von Arm erforderlich sind.


Leave a Reply
Want to join the discussion?Feel free to contribute!