A-weging equalisatie: Ontwerp en implementatie naar Arm Cortex-M devices

Ingenieurs zijn tegenwoordig in staat met behulp van moderne embedded processors, softwareframeworks en design tooling geavanceerde meetconcepten toe te passen. Een van deze toepassingen zijn slimme fabrieken als onderdeel van de I4.0 revolutie.

De laatste jaren heeft PM (predictief onderhoud) van machines veel aandacht gekregen, waarbij fabrieken hun productie-efficiëntie willen maximaliseren. Tegelijkertijd willen zij de waardevolle vaardigheden van ervaren voormannen en productiemedewerkers behouden.

Traditioneel liep een voorman rond op de werkvloer en luisterde naar de geluiden die een machine maakte. Zo kreeg hij een idee waar mogelijk een verstoring zou plaats vinden. Met de komst van I4.0 technologie kunnen nu microfoons, edge DSP-algoritmes en ML worden ingezet. Deze ‘luisteren’ naar de geluiden die een machine maakt en maken vervolgens een classificatie en voorspelling.

Een van de grootste uitdagingen is hoe je een computer kunt laten horen als een mens.

Fysica van het menselijk oor

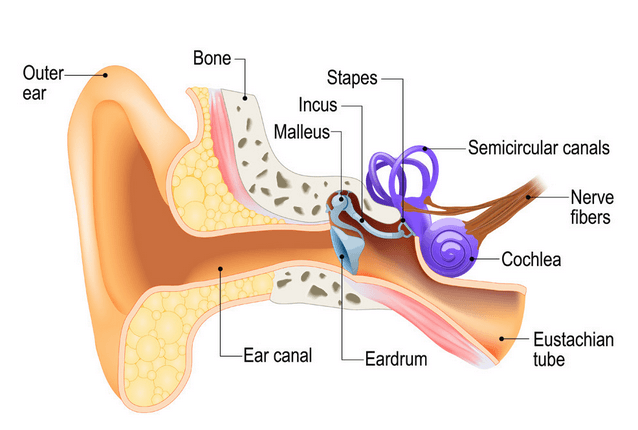
Hoe werkt het oor?

Het oor verwezenlijkt dit via drie botten (Stapes, Incus en Malleus) die fungeren als een mechanische versterker voor trillingen die worden ontvangen op het trommelvlies. Deze versterkte geluiden worden vervolgens via het Ovale venster (niet afgebeeld) naar het Cochlea gestuurd. De Cochlea (in paars weergegeven) is gevuld met een vloeistof die beweegt als reactie op de trillingen van het ovale venster. Als de vloeistof beweegt, worden duizenden zenuwuiteinden in beweging gezet. Deze zenuwuiteinden zetten geluidstrillingen om in elektrische impulsen die langs de auditieve zenuwvezels naar de hersenen gaan voor analyse.

Het modelleren van waargenomen geluid

Door de complexiteit van de vloeiende mechanische constructie van het menselijke auditieve systeem zijn lage en hoge frequenties doorgaans niet waarneembaar. Onderzoekers hebben in de loop der jaren ontdekt dat de mens het meest gevoelig is voor geluiden die in het 1-6kHz-bereik liggen. Daarbij varieert dit bereik, afhankelijk van de fysieke gezondheid van de proefpersoon.

Dit onderzoek heeft geleid tot de definitie van een set weighting curves (weegkrommes): de zogenaamde A-, B-, C- en D-weging curves, die de frequentierespons van een microfoon egaliseert. Deze weging curves hebben als doel de digitale en fysieke wereld dichter bij elkaar te brengen door een geautomatiseerd microfoonsysteem te laten horen als een mens.

De A-weging curve is de meest gebruikte, omdat deze volgens IEC-61672 op alle geluidsniveaumeters moet worden gemonteerd. De B- en D-curves worden nauwelijks gebruikt, maar de C-weging kan worden gebruikt voor het testen van de impact van geluid in telecomsystemen.

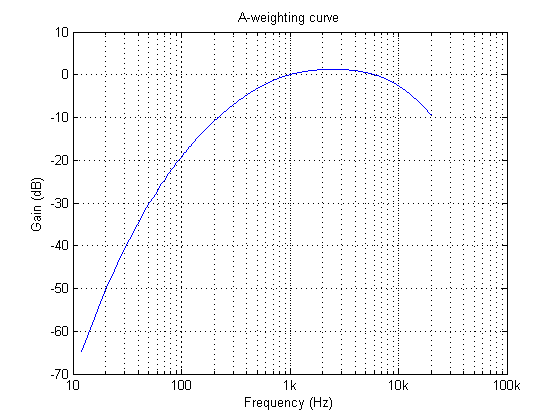
In bovenste grafiek is de frequentierespons van de A-weging curve weergegeven. De geluiden die onze oren onder 500Hz binnenkomen zijn gedefragmenteerd. Het best waarneembaar is tussen de 0.5-6kHz. Merk op dat de curve niet gespecificeerd is boven 20kHz, omdat dit het menselijke gehoorbereik overschrijdt.

ASN FilterScript

Met ASN’s FilterScript symbolische wiskunde scripttaal kunnen ontwerpers analoge filtertransferfuncties met slechts enkele regels code omzetten naar het digitale equivalent.

De analoge overdrachtsfuncties van de A- en C-weging curves staan hieronder vermeld:

\(H_A(s) \approx \displaystyle{7.39705×10^9 \cdot s^4 \over (s + 129.4)^2\quad(s + 676.7)\quad (s + 4636)\quad (s + 76655)^2}\)

\(H_C(s) \approx \displaystyle{5.91797×10^9 \cdot s^2\over(s + 129.4)^2\quad (s + 76655)^2}\)

Deze analoge transfer functies kunnen worden getransformeerd naar hun digitale equivalent door de bilinear() functie. Merk daarbij echter op dat \(H_A(s) \) een aanzienlijke hoeveelheid algebraïsche manipulatie vereist om de noemer van de coëfficiënten in machten van \(s\) te kunnen extraheren.

Convolutie

Een eenvoudige truc om polynomiale vermenigvuldiging uit te voeren is het gebruik van lineaire convolutie, wat dezelfde algebraïsche operatie is als het vermenigvuldigen van twee polynomialen samen. Dit kan eenvoudig worden uitgevoerd via Filterscript’s conv() functie:

y=conv(a,b);

Als eenvoudig voorbeeld: de vermenigvuldiging van \((s^2+2s+10)\) met \((s+5)\), wordt met 3 regels of FilterScript code gedefinieerd:

a={1,2,10};
b={1,5};
y=conv(a,b);

Dit geeft de volgende opbrengsten: 1 7 20 50 of \((s^3+7s^2+20s+50)\)

Voor de A-weging curve Laplace-transferfunctie wordt hieronder de volledige FilterScript-code gegeven:

ClearH1;  // clear primary filter from cascade

Main() // main loop

a={1, 129.4};
b={1, 676.7};
c={1, 4636};
d={1, 76655};

aa=conv(a,a); // polynomial multiplication
dd=conv(d,d);

aab=conv(aa,b);
aabc=conv(aab,c);

Na=conv(aabc,dd);
Nb = {0 ,0 , 1 ,0 ,0 , 0, 0}; // define numerator coefficients
G = 7.397e+09; // define gain

Ha = analogtf(Nb, Na, G, "symbolic");
Hd = bilinear(Ha,0, "symbolic");

Num = getnum(Hd);
Den = getden(Hd);
Gain = getgain(Hd)/computegain(Hd,1e3); // set gain to 0dB@1kHz

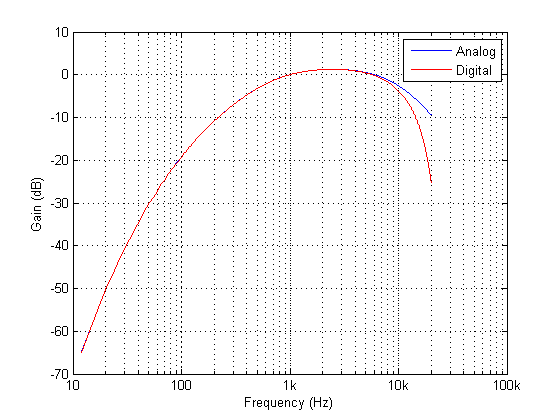
Zoals te zien is, komt de digitale equivalente magnitudereactie zeer nauw overeen met de ideale analoge magnitudereactie tot \(6kHz\).

De ITU-R 486–4 weging curve

Een andere belangrijke wegingcurve is de ITU-R 486–4 weighting curve. Deze is ontwikkeld door de BBC. In tegenstelling tot het A-weging curve filter beschrijft de ITU-R 468-4-curve de subjectieve luidheid voor breedbandstimuli. Het belangrijkste nadeel van de A-weging curve is dat deze de luidheidsevaluatie van reële stimuli onderschat, met name in de frequentieband van ongeveer 1-9 kHz.

Door de precieze definitie van de 486-4 wegingscurve is er geen analoge transfer functie beschikbaar. In plaats daarvan biedt de standaard een tabel met amplitudes en frequenties – hier weergegeven. Deze specificatie kan rechtstreeks worden ingevoerd in Filterscript’s firarb() functie om een geschikt FIR filter te ontwerpen, zie hieronder:

ClearH1;  // clear primary filter from cascade
ShowH2DM;

interface L = {10,400,10,250}; // filter order

Main()

// ITU-R 468 Weighting
A={-29.9,-23.9,-19.8,-13.8,-7.8,-1.9,0,5.6,9,10.5,11.7,12.2,12,11.4,10.1,8.1,0,-5.3,-11.7,-22.2};
F={63,100,200,400,800,1e3,2e3,3.15e3,4e3,5e3,6.3e3,7.1e3,8e3,9e3,1e4,1.25e4,1.4e4,1.6e4,2e4};

A={-30,A};  //  specify arb response
F={0,F,fs/2};   //

Hd=firarb(L,A,F,"blackman","numeric");

Num=getnum(Hd);
Den={1};
Gain=getgain(Hd);

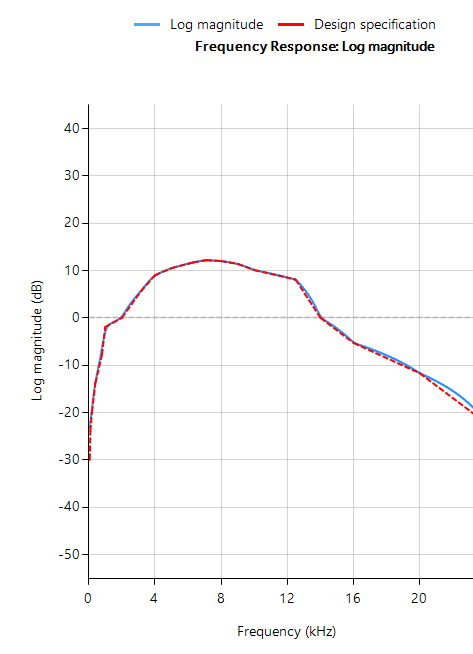
Frequentierespons van een ITU-R 468-4 FIR-filter ontworpen met Filterscript’s firarb() functie voor \(f_s=48kHz\)

Zoals te zien, biedt FilterScript de ontwerper een zeer krachtige symbolische scripttaal voor het ontwerpen van weeg curve filters. Nu volgt een bespreking van de implementatie van een A-weeg curve filter op een Arm gebaseerde processor via de automatische codegenerator van de tool. De concepten en stappen die hieronder worden gedemonstreerd gelden ook voor FIR-filters.

Automatische code generatie naar Arm processor cores via CMSIS-DSP

Het filter ontwerp kan nu met de automatische codegeneratie-engine van de ASN Filter Designer nu geexporteerd worden naar een Cortex-M Arm-gebaseerde processor via het CMSIS-DSP software raamwerk. De ingebouwde analyse- en helpfuncties van de tool helpen de ontwerper bij het succesvol configureren van het ontwerp voor implementatie.

Voordat de code wordt gegenereerd, moet het H2-filter (d.w.z. het filter dat in FilterScript is ontworpen) eerst opnieuw worden geoptimaliseerd (getransformeerd) naar een H1-filter (hoofdfilter) structuur voor gebruik. Het optiemenu is te vinden onder de P-Z tab in de hoofd UI.

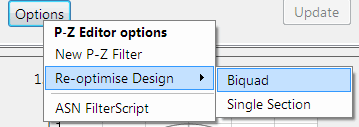
Alle ontwerpen van IIR-filters met floating point moeten gebaseerd zijn op Single Precision arithmetic en ofwel een Direct Form I of Direct Form II getransponeerde filterstructuur hebben. De Direct Form II getransponeerde structuur wordt geadviseerd voor floating point implementatie vanwege de hogere numerieke nauwkeurigheid.

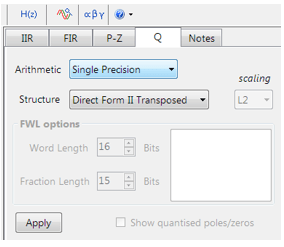
De instellingen voor kwantisatie en de filterstructuur zijn te vinden onder het tabblad Q (zoals links afgebeeld). Door Arithmetic op Single Precision te zetten en Structure op Direct Form II Transposed en vervolgens op Apply te klikken, wordt de IIR voor het CMSIS-DSP software raamwerk geconfigureerd.

Selecteer het Arm CMSIS-DSP raamwerk in het selectievakje in het filteroverzichtsvenster:

De automatisch gegenereerde C-code op basis van het CMSIS-DSP framework voor directe implementatie op een Arm-gebaseerde Cortex-M processor staat hieronder weergegeven:

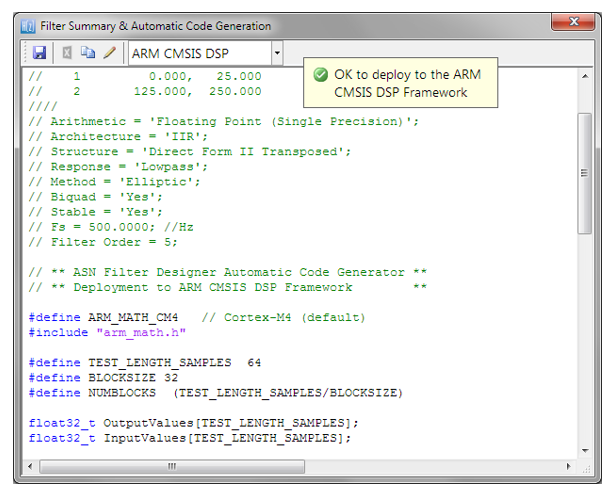
Zoals weergegeven, genereert de automatische codegenerator van de ASN Filter Designer alle initialisatiecode, schaling en datastructuren die nodig is om het A-weighting IIR-filter te implementeren via de CMSIS-DSP-bibliotheek van Arm.