Upgraden van verouderde ontwerpen gebaseerd op analoge filters
Analoge filters bestaan al sinds het begin van elektronica, variërend van eenvoudige inductor-capacitor netwerken tot meer geavanceerde actieve filters met op-amps; beproefde legacy filterontwerpen voor een breed scala aan sensormeettoepassingen. Digitale filters die geïntegreerd zijn in de applicatiecode van de microcontroller zijn echter de norm geworden vanwege de prestatie-eisen van moderne IoT (Internet of Things) sensormeettoepassingen. En daarnaast vanwege de lagere productkosten. Maar hoe krijgen we het beste van twee werelden?
Ontwerpers hoeven niet het wiel op opnieuw uit te vinden. Ze kunnen een bestaande analoge filtertransferfunctie nemen en deze transformeren naar digitaal (via een transformatie). Deze kan vervolgens als digitaal filter geïmplementeerd worden in een microcontroller of DSP (digitale signaalprocessor). Transformaties van analoog naar digitaal bestaan al tientallen jaren. De beschikbaarheid van DSP-ontwerphulpmiddelen voor het aanpassen van het “getransformeerde digitale filter” is echter enigszins beperkt, wat het ontwerp- en validatieproces belemmert.
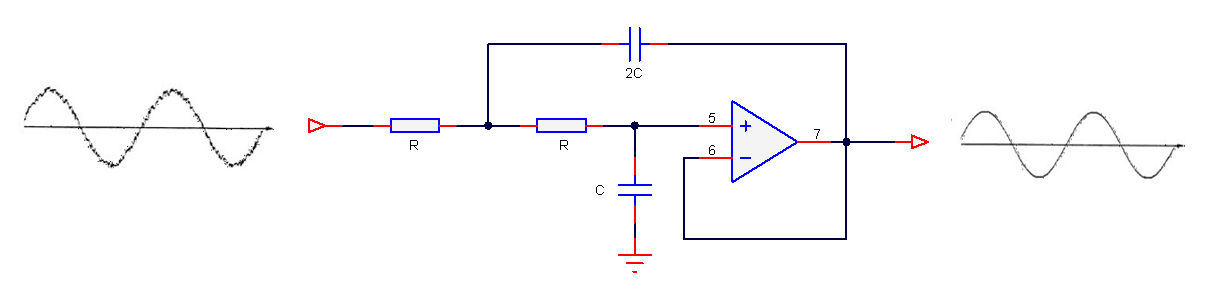
Een 2e orde analoog laagdoorlaatfilter is hieronder afgebeeld. In zijn simpelste vorm zijn er slechts 5 componenten nodig om het filter te bouwen. Dit klinkt eenvoudig, toch?
The pros
Het meest voor de hand liggende voordeel is dat analoge filters een uitstekende resolutie hebben, aangezien er geen rekening hoeft te worden gehouden met het “aantal bits”. Analoge filters hebben goede EMC (elektromagnetische compatibiliteit) eigenschappen, omdat er geen klok genererende ruis is. Er zijn geen effecten van aliasing, wat zeker geldt voor de eenvoudigere op-amps. Deze hebben geen fancy chopping of auto-calibration schakelingen in zich. En analoge ontwerpen kunnen goedkoop zijn, belangrijk wanneer kosten voor een toepassing belangrijk zijn.
Klinkt goed, maar wat is het slechte nieuws?
Analoge filters hebben een aantal belangrijke nadelen die de filterprestaties beïnvloeden. Zoals veroudering van componenten, temperatuurdrift en componenttolerantie. Bovendien vergt een goede prestatie goede analoge ontwerpvaardigheden en een goede PCB (printed circuit board) layout, welke moeilijk te vinden zijn.
Deze nadelen maken digitale filters erg geschikt voor moderne toepassingen die een hoge herhaalbaarheid van karakteristieken vereisen. Een voorbeeld: stel dat u 1000 meetmodules wilt vervaardigen nadat u uw filterontwerp hebt geoptimaliseerd. Met een digitale oplossing kunt u er zeker van zijn dat de prestaties van uw filter in alle modules identiek zijn. Dit is zeker niet het geval bij analoge oplossingen, omdat de tolerantie van de componenten, de veroudering van de componenten en de temperatuurdrift tot gevolg hebben dat het filter van elke module zijn eigen karakteristieken zal hebben. Bovendien blijft de frequentierespons van een analoog filter vast, oftewel een Butterworth-filter zal altijd een Butterworth-filter blijven. Om de frequentierespons te wijzigen, moeten de componenten op de printplaat fysiek worden gewijzigd, wat niet ideaal is!
Digitale filters zijn adaptief en flexibel. We kunnen een filter ontwerpen en implementeren met elke frequentierespons die we willen, het inzetten en dan de filtercoëfficiënten bijwerken zonder iets op de printplaat te veranderen! Het is ook gemakkelijk om digitale filters te ontwerpen met lineaire fase en bij zeer lage bemonsteringsfrequenties – twee dingen die lastig zijn bij analoog.
Laplace naar discrete/digitale transformaties
De drie hier besproken methoden houden in wezen in dat een (analoge) Laplace-overdrachtsfunctie, \(H(s)\) wordt omgezet in een discrete overdrachtsfunctie, \(H(z)\) ), zodat een analoog filter dat reeds in een ontwerp wordt gebruikt, kan worden geïmplementeerd op een microcontroller of DSP.
Een aantal nuttige Laplace-naar-Z-transformaties staan in onderstaande tabel weergegeven:
\(
\begin{array}{ccc}\hline
H(s) &\longleftrightarrow & H(z) \\ \hline
1 &\longleftrightarrow & 1 \\
\frac{\displaystyle1}{\displaystyle s}
&\longleftrightarrow& \frac{\displaystyle 1}{\displaystyle 1-z^{\scriptstyle -1}}\\
\frac{\displaystyle 1}{\displaystyle s^{\scriptstyle 2}} &\longleftrightarrow& \frac{\displaystyle
Tz^{\scriptstyle-1}}{\displaystyle (1-z^{\scriptstyle -1})^2}\\
\frac{\displaystyle 1}{\displaystyle s+a}
&\longleftrightarrow&
\frac{\displaystyle 1}{\displaystyle 1-e^{-aT}z^{-1}}\\
\frac{\displaystyle 1}{\displaystyle (s+a)^2}
&\longleftrightarrow& \frac{\displaystyle z^{-1}(1-e^{-aT})}{\displaystyle a(1-z^{-1})(1-e^{-aT}z^{-1})}\\\hline
\end{array}
\)
A table of useful Laplace and z-transforms
Bilineaire z-transformatie (BZT)
De bilineaire z-transformatie (BZT) zet eenvoudig een analoge overdrachtsfunctie, \(H(s)\) , om in een discrete overdrachtsfunctie, \(H(z)\) door alle \(s\)-termen te vervangen door het volgende:
\(\displaystyle
s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} \label{bzt}\)
Waarbij \(T\) de bemonsteringsperiode van het discrete systeem is. Wanneer echter \(s=j\Omega\) en \(z=e^{jwT}\) in de BZT-vergelijking worden gesubstitueerd en vereenvoudigd, blijkt dat er in feite een niet-lineair verband bestaat tussen de analoge, \(\Omega\) en discrete, \(w\) frequenties. Dit verband wordt hieronder getoond en is het gevolg van de niet-lineariteit van de arctangensfunctie.
\(\displaystyle
\omega=2\tan^{-1}\left(\frac{\Omega T}{2}\right)
\label{bzt_warp_def1}
\)
Bij analyse van de vergelijking blijkt dat de gelijkmatig verdeelde analoge frequenties in het bereik – \(-\infty<\Omega<\infty\) op niet-lineaire wijze worden gecomprimeerd in het frequentiebereik \(-\pi<w<\pi\) n het discrete domein. Deze relatie wordt frequentievervorming genoemd, en kan worden gecompenseerd door de analoge frequenties vooraf te vervormen door:
\(\displaystyle
\Omega_c=\frac{2}{T}\tan\left(\frac{\Omega_d T}{2}\right)
\label{bzt_warp_def2}
\)
waarbij \(\displaystyle\Omega_c\) de gecompenseerde of voorgefilterde analoge frequentie is, en \(\displaystyle\Omega_d\) de gewenste analoge frequentie.
Het ASN FilterScript commando \(\texttt{bilinear}\) kan worden gebruikt om een Laplace overdrachtsfunctie om te zetten in zijn discrete equivalent met behulp van de BZT transformatie. Hieronder wordt een voorbeeld gegeven.
Impulsinvariante methode
De tweede transformatie wordt immpulsinvariante methode (Impulse Invariant Transform, IIT) genoemd, omdat de polen van de Laplace overdrachtsfunctie worden omgezet in hun discrete equivalenten. Zodat de discrete impulsrespons, \(h(n)\) identiek is aan een regelmatig bemonsterde representatie van de analoge impulsrespons. (Dat wil zeggen: \(h(n)=h(nT)\), waarbij \(T\) de bemonsteringsfrequentie is, en \(t=nT\)). De IIT is een veel omslachtigere omzettingstechniek dan de BZT, omdat de Laplace-overdrachtsfunctie eerst moet worden uitgebreid met partiële breuken voordat de transformatie toe te passen.
De transformatietechniek wordt hieronder gedefinieerd:
\(\displaystyle
\frac{K}{s+a} \quad\longrightarrow\quad
\frac{K}{1-e^{-aT}z^{-1}} \label{iit_def}
\)
Deze methode heeft meerdere beperkingen, aangezien geen transformatie van nullen of afzonderlijke constante termen (na expansie) mogelijk is. En zij moet een hoge bemonsteringsfrequentie hebben om de effecten van spectrale aliasing te ondervangen. De effecten van aliasing hinderen deze methode aanzienlijk. Daarom mag de methode alleen worden gebruikt wanneer de vereiste is dat de impulsrespons van de analoge overdrachtsfunctie overeenkomt, aangezien het resulterende discrete model een ander magnitude- en fasespectrum (frequentierespons) kan hebben dan dat van het oorspronkelijke analoge systeem. Daardaar is de impulseinvariante methode ongeschikt voor het modelleren van hoogdoorlaatfilters, en is zij derhalve beperkt tot het modelleren van laagdoorlaat- of banddoorlaatfilters.
Vanwege de bovengenoemde beperkingen van de IIT-methode wordt deze momenteel niet ondersteund in ASN Filterscript.
De matched-z transformatie
Een andere techniek van het analoog naar discreet modelleren is de matched-z transformatie. Zoals de naam al aangeeft, zet de transformatie de polen en nullen van de analoge overdrachtsfunctie direct om in polen en nullen in het z-vlak. De transformatie wordt hieronder beschreven, waarbij \(T\) de bemonsteringsfrequentie is.
\(\displaystyle
\frac{\prod\limits_{k=1}^q(s+b_k)}{\prod\limits_{k=1}^p(s+a_k)}
\quad\longrightarrow\quad
\frac{\prod\limits_{k=1}^q(1-e^{-b_kT}z^{-1})}{\prod\limits_{k=1}^p(1-e^{-a_kT}z^{-1})}
\label{matchedz_def}
\)
Uit analyse van de transformatievergelijking blijkt dat de getransformeerde polen in het z-vlak identiek zullen zijn aan de polen verkregen met de impulsinvariante methode. Merk echter op dat de posities van de nullen verschillend zullen zijn, omdat de impulsinvariante methode ze niet kan transformeren.
Het ASN Filterscript commando \(\texttt{mztrans}\) is beschikbaar voor deze methode.
Een gedetailleerd voorbeeld
Om het gemak van het transformeren van analoge filters in hun discrete/digitale equivalenten met behulp van de analoog naar discrete transformaties aan te tonen, volgt nu een voorbeeld van modellering met de BZT voor een analoog 2e orde laagdoorlaatfilter.
Een veralgemeend 2e orde analoog laagdoorlaatfilter wordt gegeven door:
\(\displaystyle
H(s)=\frac{w_c^2}{s^2+2\zeta w_c s + w_c^2}
\)
waarbij \(w_c=2\pi f_c\) de afsnijfrequentie is en \(\zeta\) de demping van het filter bepaalt, waarbij \(\zeta=1/\sqrt{2}\) kritisch gedempt wordt genoemd of gelijk aan to -3dB bij \(w_c\). Veel analoge ingenieurs kiezen ervoor om voor hun ontwerpen een kwaliteitsfactor, \(Q = \displaystyle\frac{1}{2\zeta}\) of piekfactor te specificeren. Als we\(Q\) in \(H(s)\) invoegen, verkrijgen we:
\(\displaystyle
H(s)=\frac{w_c^2}{s^2+ \displaystyle{\frac{w_c}{Q}s} + w_c^2}
\)
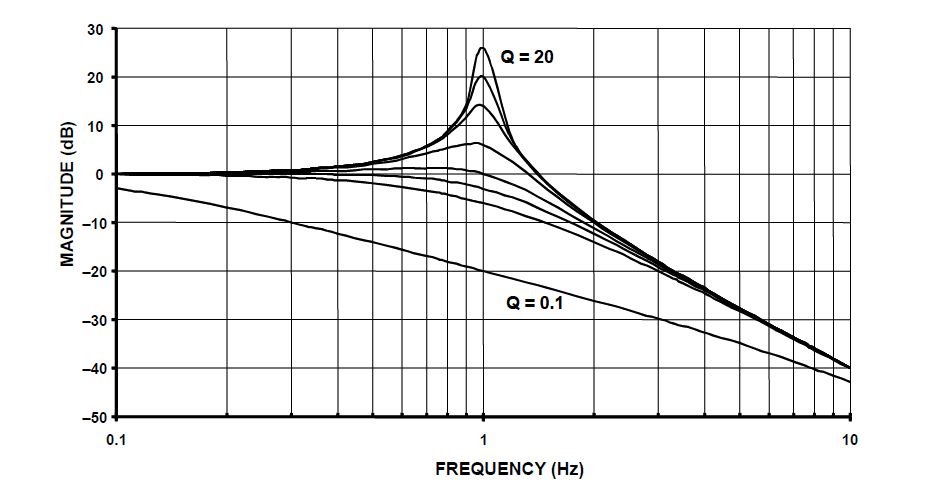
Bij analyse van \(H(s)\) blijkt dat \(Q=1/\sqrt{2} = 0.707\) ook een kritisch gedempte respons oplevert. Verschillende waarden van \(Q\) worden hieronder weergegeven. Zoals te zien is dat als \(Q>1/\sqrt{2}\) piekvorming optreedt.
Prototype magnitudespectrum van het 2e orde laagdoorlaatfilter voor verschillende waarden van Q:
Merk op dat wanneer \(Q>1/\sqrt{2}\) piekvorming optreedt.
Voordat de BZT in ASN FilterScript wordt toegepast, moet de analoge overdrachtsfunctie in een analoog filterobject worden gespecificeerd. De volgende code maakt een analoog filterobject voor het hier beschouwde 2e orde laagdoorlaat-prototype:
Main()
wc=2*pi*fc;
Nb={0,0,wc^2};
Na={1,wc/Q,wc^2};
Ha=analogtf(Nb,Na,1,"symbolic"); // make analog filter object
Het \(\texttt{symbolic}\) keyword genereert een symbolische weergave van de overdrachtsfunctie in het commandovenster. Voor een bemonsteringsfrequentie van \(f_s=500Hz\) en \(f_c=30Hz\) en \(Q=0.707\) verkrijgen we:
Toepassing van de BZT via het bilineair \(\texttt{bilinear}\) commando zonder prewarping,
Hd=bilinear(Ha,0,"symbolic");
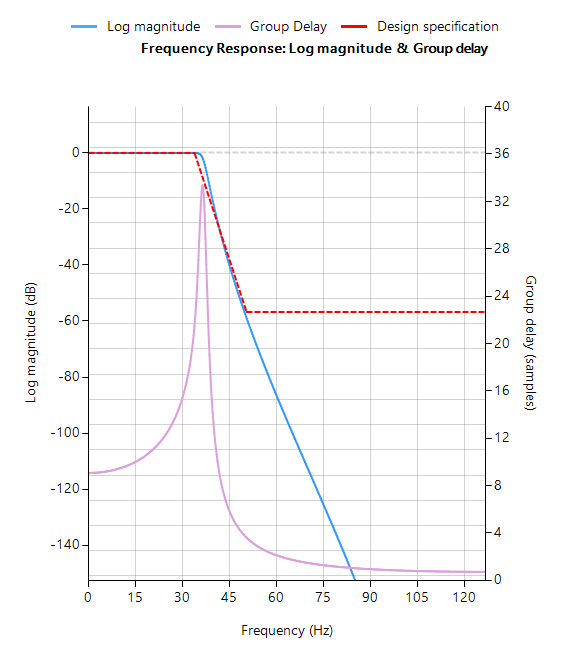
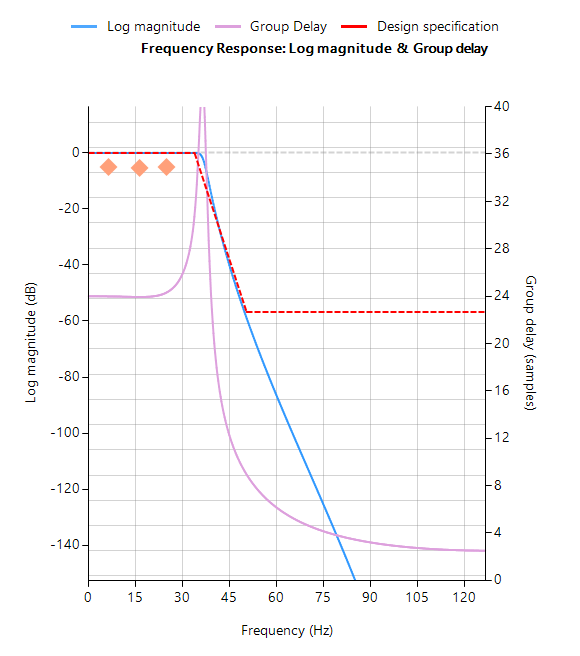
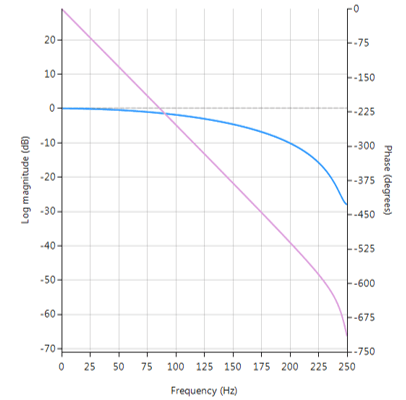
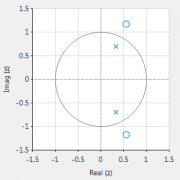
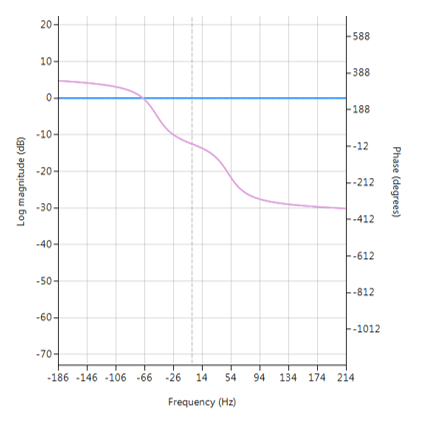
De volledige frequentierespons van het getransformeerde digitale filter staat hieronder, waarbij te zien is dat bij \(30Hz\) de magnitude \(-3dB\) is en de fase \( -90^{\circ}\), zoals verwacht. Merk ook op hoe de magnitude roll-off van het filter wordt beïnvloed door het dubbele nulpaar bij Nyquist (zie de z-vlak grafiek hieronder), wat leidt tot verschillen met zijn analoge neef. 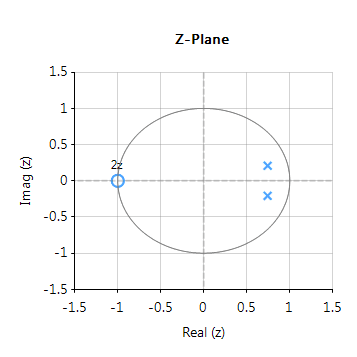
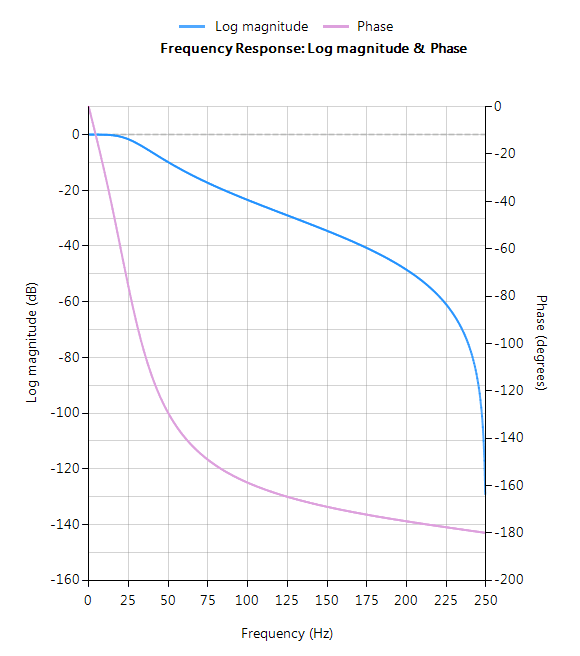
De pool-nul posities kunnen worden getweaked binnen ASN Filterscript of via de ASN Filter Designer’s interactieve pool-nul z-vlak plot editor door alleen de muis te gebruiken!
Implementatie
De volledige code voor het omzetten van een veralgemeend 2e orde analoog laagdoorlaatfilter prototype in zijn digitale equivalent met behulp van de BZT via ASN FilterScript staat hieronder weergegeven:
ClearH1; // clear primary filter from cascade
interface Q = {0.1,10,0.02,0.707};
interface fc = {10,200,10,40};
Main()
wc=2*pi*fc;
Nb={0,0,wc^2};
Na={1,wc/Q,wc^2};
Ha=analogtf(Nb,Na,1,"symbolic"); // make analog filter object
Hd=bilinear(Ha,0,"symbolic"); // transform Ha via BZT into digital object, Hd
Num=getnum(Hd);
Den=getden(Hd);
Gain=getgain(Hd);