Les filtres IIR (réponse impulsionnelle infinie) sont généralement choisis pour les applications où la phase linéaire n’est pas trop importante et où la mémoire est limitée. Ils ont été largement déployés dans l’égalisation audio, le traitement du signal des capteurs biomédicaux, les capteurs intelligents IoT/IIoT et les applications de télécommunication/RF à haut débit, et constituent une composante essentielle de la conception algorithmique.
Avantages
- Faible empreinte de mise en œuvre : nécessite moins de coefficients et de mémoire que les filtres FIR afin de satisfaire un ensemble similaire de spécifications, à savoir la fréquence de coupure et l’atténuation de la bande d’arrêt
- Faible latence : convient au contrôle en temps réel et aux applications RF à très haut débit en raison de la faible empreinte des coefficients
- Peut être utilisé pour imiter les caractéristiques des filtres analogiques en utilisant des transformations de mappage dans le plan s-z
Inconvénients
- Caractéristiques de phase non linéaires
- Nécessite plus d’analyse de mise à l’échelle et de débordement numérique lorsqu’il est implémenté en virgule fixe
- Moins stables numériquement que leurs homologues RIF (réponse impulsionnelle finie), en raison des chemins de rétroaction
Définition
Un filtre RII est catégorisé par sa réponse impulsionnelle théoriquement infinie,
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)
En pratique, il n’est pas possible de calculer la sortie d’un IIR à l’aide de cette équation. Par conséquent, l’équation peut être réécrite en termes d’un nombre fini de pôles \(p\) et de zéros \(q\), comme défini par l’équation de différence linéaire à coefficient constant donnée par:
y(n)=\sum_{k=0}^{q}b(k)x(n-k)-\sum_{k=1}^{p}a(k)y(n-k)
\)
où \(a(k)\) et \(b(k)\) sont les coefficients polynomiaux du dénominateur et du numérateur du filtre, dont les racines sont respectivement égales aux pôles et aux zéros du filtre. Ainsi, une relation entre l’équation de différence et la transformée en z (fonction de transfert) peut donc être définie en utilisant la propriété de retard de la transformée en z telle que,
\sum_{k=0}^{q}b(k)x(n-k)-\sum_{k=1}^{p}a(k)y(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b(k)z^{-k}}{1+\sum\limits_{k=1}^p a(k)z^{-k}}
\)
Comme on le voit, la fonction de transfert est une représentation du filtre dans le domaine fréquentiel. Remarquez également que les pôles agissent sur les données de sortie, et les zéros sur les données d’entrée. Puisque les pôles agissent sur les données de sortie et affectent la stabilité, il est essentiel que leurs rayons restent à l’intérieur du cercle unitaire (c’est-à-dire <1) pour la stabilité BIBO (bounded input, bounded output). Les rayons des zéros sont moins critiques, car ils n’affectent pas la stabilité du filtre. C’est la principale raison pour laquelle les filtres FIR (réponse impulsionnelle finie) tout-zéro sont toujours stables.
Vous trouverez ici une discussion sur les structures de filtres RII en virgule fixe et en virgule flottante.
Méthodes classiques de conception de filtres RII
Nous allons maintenant discuter des méthodes de conception IIR les plus couramment utilisées ou classiques (Butterworth, Chebyshev et Elliptique). Pour ceux qui cherchent des exemples plus généraux, veuillez visiter le ASN-Blog pour les nombreux articles sur le sujet.
Le concepteur graphique d’ASN Filter Designer supporte la conception des quatre méthodes classiques de conception RII suivantes:
- Butterworth
- Chebyshev de Type I
- Chebyshev de Type II
- Elliptique
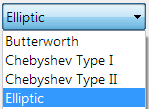
L’algorithme utilisé pour le calcul conçoit d’abord un filtre analogique (via un prototype de conception analogique) avec les spécifications de filtre souhaitées spécifiées par les marqueurs de conception graphique – c’est-à-dire l’ondulation et les fréquences de coupure passe/bande d’arrêt. Le filtre analogique résultant est ensuite transformé par la transformation Bilinéaire en Z en son équivalent discret pour être réalisé.
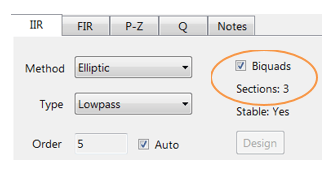

Les implémentations Biquad sont préconisées pour la stabilité numérique.

Le prototype de Bessel n’est pas pris en charge, car la transformée bilinéaire déforme les caractéristiques de phase linéaire. Cependant, une méthode de conception de filtre de Bessel est disponible dans ASN FilterScript .
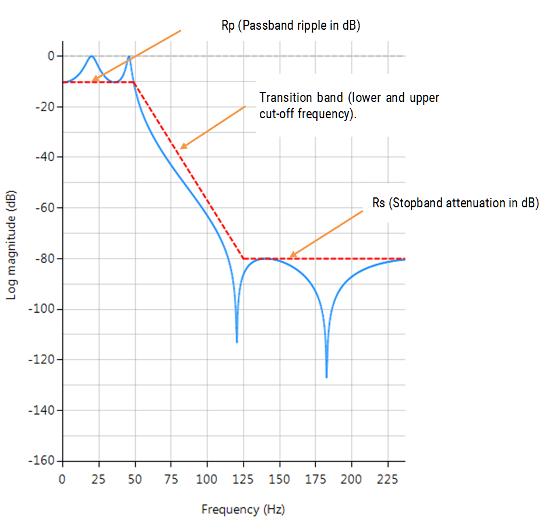
Comme discuté ci-dessous, chaque méthode a ses avantages et ses inconvénients, mais en général la méthode Elliptique devrait être considérée comme le premier choix car elle répond aux spécifications de conception avec l’ordre le plus bas de toutes les méthodes. Cependant, cette propriété souhaitable se fait au prix d’une ondulation dans la bande passante et la bande d’arrêt, et de caractéristiques de phase de bande passante très non linéaires. Par conséquent, le filtre elliptique ne doit être utilisé que dans les applications où la mémoire est limitée et où la linéarité de la phase de la bande passante est moins importante.
Les méthodes Butterworth et Tchebychev de type II ont des bandes passantes plates (sans ondulation), ce qui en fait un bon choix pour les applications de mesure en courant continu et à basse fréquence, comme les capteurs à pont (par exemple, les capteurs de charge). Cependant, cette propriété souhaitable se fait au détriment de bandes de transition plus larges, ce qui se traduit par une faible transition bande passante-bande d’arrêt (roll-off lent). Les méthodes de Chebyshev de type I et Elliptique ont un amortissement plus rapide mais présentent une ondulation de la bande passante et des caractéristiques de phase de bande passante très non linéaires.
Comparaison des méthodes de conception classiques
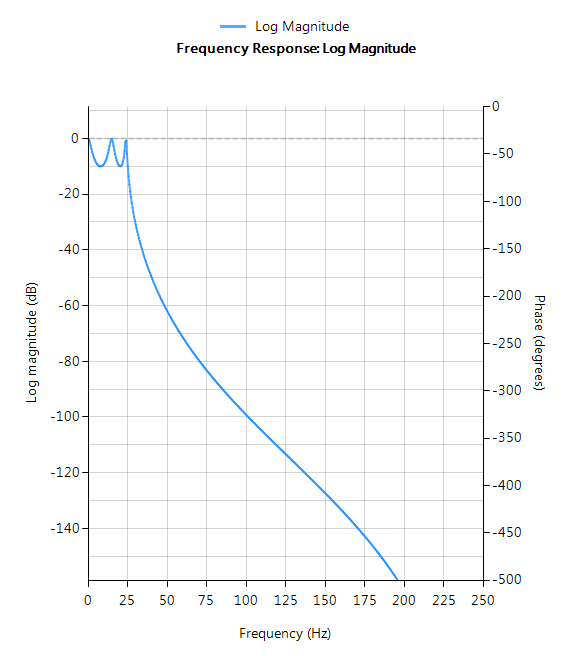
Les diagrammes de réponse en fréquence illustrés ci-dessous montrent les différences entre les diverses méthodes de conception prototypes pour un filtre passe-bas d’ordre 5 avec les mêmes spécifications. Comme on le voit, la réponse de Butterworth est la plus lente à s’atténuer et celle d’Elliptic la plus rapide.
Elliptique
Les filtres elliptiques offrent des caractéristiques de coupure plus abruptes que les filtres Butterworth ou Tchebychev, mais sont équiréparables dans la bande passante et la bande d’arrêt. En général, les filtres elliptiques répondent aux spécifications de conception avec l’ordre le plus bas de toutes les méthodes discutées ici.
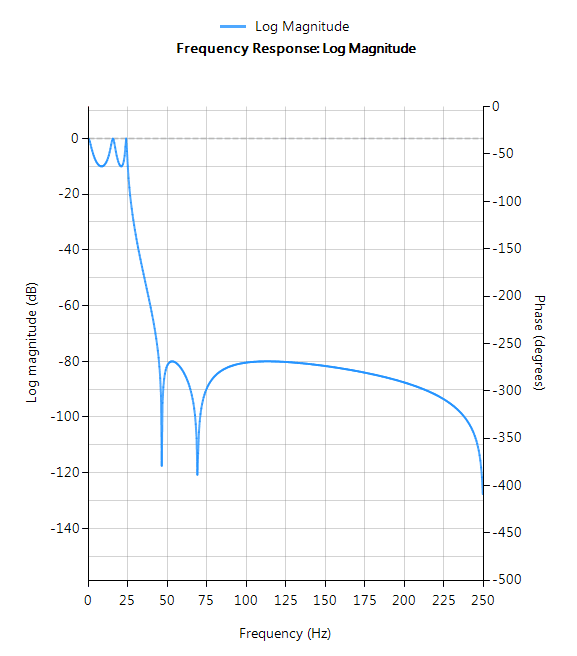
Caractéristiques du filtre
- Décroissance la plus rapide de tous les prototypes supportés
- Equiréflexion dans la bande passante et la bande d’arrêt
- Filtre d’ordre le plus bas de tous les prototypes pris en charge
- Caractéristiques de phase non linéaires dans la bande passante
- Bon choix pour les applications de contrôle en temps réel et à haut débit (applications RF)
Butterworth
Les filtres de Butterworth ont une réponse en amplitude extrêmement plate dans la bande passante et monotone dans l’ensemble, ce qui en fait un bon choix pour les applications de mesure en courant continu et à basse fréquence, telles que les capteurs de charge. Toutefois, cette “douceur” hautement souhaitable se paie au prix d’une diminution de la pente de décroissance. En conséquence, la méthode de Butterworth présente les caractéristiques de décroissance les plus lentes de toutes les méthodes discutées ici.
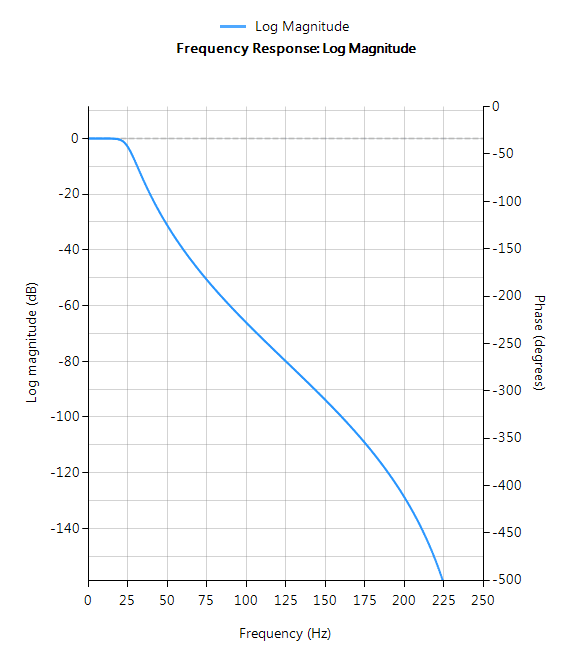
Caractéristiques du filtre
- Réponse monotone lisse (pas d’ondulation)
- Décroissance la plus lente pour un ordre équivalent
- Ordre le plus élevé de tous les prototypes supportés
- Réponse en phase de la bande passante plus linéaire que toutes les autres méthodes
- Bon choix pour les mesures de courant continu et les applications audio
Chebyshev de Type I
Les filtres de Chebyshev de type I sont équirépondants dans la bande passante et monotones dans la bande d’arrêt. En tant que tels, les filtres de type I s’annulent plus rapidement que les filtres de Chebychev de type II et de Butterworth, mais au prix d’une plus grande ondulation de la bande passante.
Caractéristiques du filtre
- Ondulation de la bande passante
- Bande d’arrêt maximalement plate
- Décroissance plus rapide que Butterworth et Chebyshev de type II
- Bon compromis entre Elliptique et Butterworth
Chebyshev de Type II
Les filtres Chebyshev de type II sont monotones dans la bande passante et équirépartissables dans la bande d’arrêt, ce qui en fait un bon choix pour les applications de capteurs à pont. Bien que les filtres conçus à l’aide de la méthode de type II soient plus lents à s’annuler que ceux conçus à l’aide de la méthode de Chebyshev de type I, l’annulation est plus rapide que celle des filtres conçus à l’aide de la méthode de Butterworth.
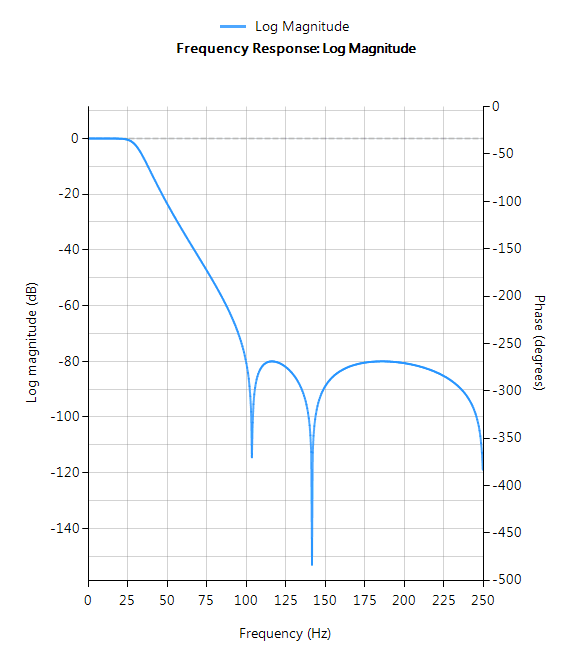
Caractéristiques du filtre
- Bande passante maximalement plate
- Décroissance plus rapide que Butterworth
- Retombée plus lente que celle Chebyshev de type I
- Bon choix pour les applications de mesure en courant continu