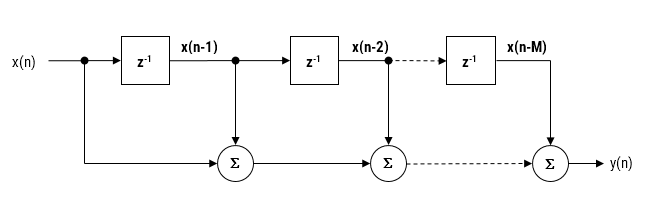
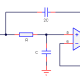
Der Filter des gleitenden Durchschnitts

Der Filter des gleitenden Durchschnitts (auch gleitender Mittelwert) ist vielleicht einer der am häufigsten verwendeten FIR-Filter aufgrund seiner konzeptionellen Einfachheit und leichten Implementierung. Wie im Diagramm unten zu sehen, ist zu beachten, dass der Filter keine Multiplikationen benötigt. Nur Additionen und eine Verzögerungsleitung. Das macht ihn sehr geeignet für viele extrem stromsparende eingebettete Geräte mit einfachen Rechenfähigkeiten.

Trotz seiner Einfachheit ist das Filter des gleitenden Durchschnitts optimal geeignet, um Rauschen zu reduzieren und gleichzeitig eine scharfe Sprungantwort beizubehalten, was es zu einem vielseitigen Baustein für intelligente Sensorsignalverarbeitungsanwendungen macht.

Ein Filter mit gleitendem Durchschnitt der Länge \(L\) für ein Eingangssignal \(x(n)\) kann wie folgt definiert werden:

\(y(n)=\large{\frac{1}{L}}\normalsize{\sum\limits_{k=0}^{L-1}x(n-k)}\) for \(\normalsize{n=0,1,2,3….}\)

Dabei besagt eine einfache Faustregel, dass der Betrag der Rauschunterdrückung gleich der Quadratwurzel aus der Anzahl der Punkte im Mittelwert ist. Zum Beispiel führt ein Filter des gleitenden Durchschnitts der Länge 9 zu einer Rauschunterdrückung um den Faktor 3.

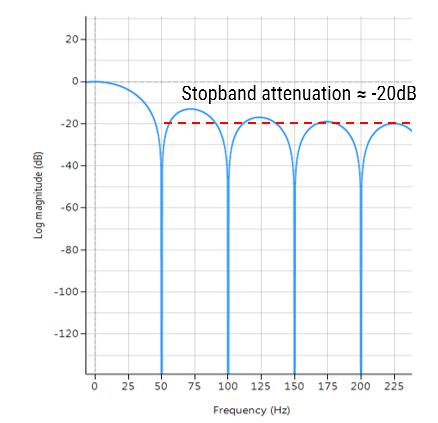
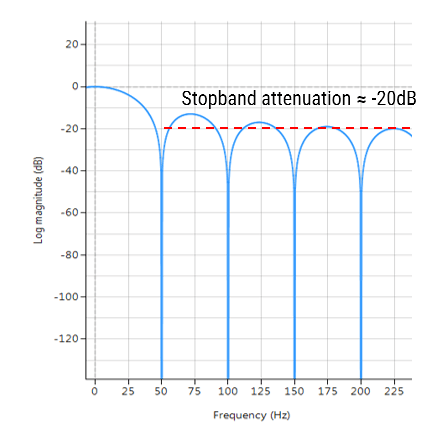Frequenzgang eines Filters des gleitenden Durchschnitts-Filters der Länge 9. Beachten Sie die schlechte Dämpfung des Sperrbereichs bei etwa -20 dB.

Vorteile

Das am häufigsten verwendete digitale Tiefpassfilter
Optimal für die Reduzierung von Rauschen unter Erhaltung einer scharfen Sprungantwort
Gute Glättung (Zeitbereich)
Einwertige Filterkoeffizienten, keine MAC-Operationen (Multiplizieren und Akkumulieren) erforderlich.
Konzeptionell einfach zu implementieren

Nachteile

Unflexibler Frequenzgang: das Verschieben eines konjugierten Nullpunktpaares führt zu nicht-einheitlichen Koeffizienten
Schlechtes Tiefpassfilter (Frequenzbereich): langsamer Roll-Off und schlechte Dämpfungseigenschaften im Sperrbereich

Implementierung

Der Filter des gleitenden Durchschnitts kann in span style=”color: #0000ff;”>ASN FilterScript wie folgt implementiert werden:

ClearH1;  // clear primary filter from cascade
Main();
Hd=movaver(8,"symbolic");  // design an 8th order MA
Num = getnum(Hd);   // define numerator coefficients
Den = {1};          // define denominator coefficients
Gain = getgain(Hd); // define gain

Eine rechnerisch effizientere Implementierung des Filters des gleitenden Durchschnitts wird hier diskutiert.

Weitere Information

Understanding Digital Signal Processing, Chapter 5, R. G. Lyons
The Scientist and Engineer’s Guide to Digital Signal Processing, Chapter 15, Steven W. Smith