Un filtre numérique est un algorithme mathématique qui opère sur un ensemble de données numériques (par exemple, des données de capteur) afin d’extraire les informations intéressantes et de supprimer toute information indésirable. Parmi les applications de ce type de technologie, citons la suppression des anomalies dans les données de capteurs ou même le nettoyage du bruit sur un signal mesuré pour faciliter l’analyse des données. Mais comment choisir le meilleur type de filtre numérique pour notre application ? Et quelles sont les différences entre un filtre RII et un filtre RIF?
Les filtres numériques sont divisés en deux catégories :
- Réponse impulsionnelle infinie (RII)
- Réponse impulsionnelle finie (RIF)
Comme leur nom l’indique, chaque type de filtre est classé en fonction de la longueur de sa réponse impulsionnelle. Toutefois, avant de commencer une analyse mathématique détaillée, il est prudent d’apprécier les différences de performances et de caractéristiques de chaque type de filtre.
Exemple
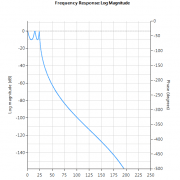
Afin d’illustrer les différences entre un RII et un RIF, la réponse en fréquence d’un RIF d’ordre 14 (ligne pleine) et d’un RII de type I de Chebyshev d’ordre 4 (ligne pointillée) est présentée ci-dessous à la figure 1. Remarquez que bien que les spectres d’amplitude aient un degré d’atténuation similaire, le spectre de phase du filtre RII est non linéaire dans la bande passante (\(\small 0\rightarrow7.5Hz\)), et devient très non linéaire à la fréquence de coupure, \(\small f_c=7.5Hz\). Notez également que le filtre RIF nécessite un plus grand nombre de coefficients (15 contre 10 pour le RII) pour correspondre aux caractéristiques d’atténuation du RII.
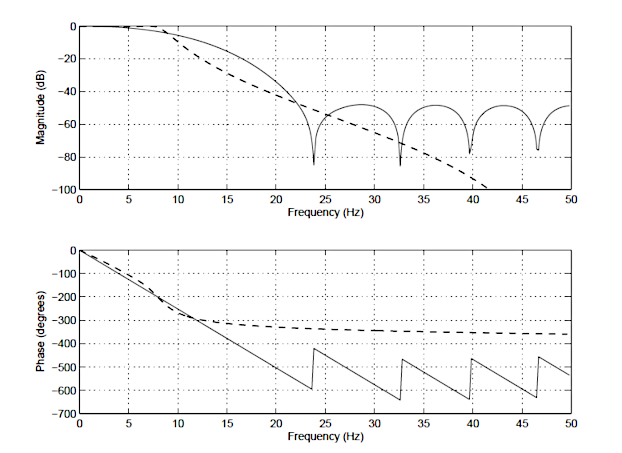
Ce ne sont là que quelques-unes des différences entre les deux types de filtres. Un résumé détaillé des principaux avantages et inconvénients de chaque type de filtre va maintenant suivre.
Filtres RII
Les filtres RII (Réponse impulsionnelle infinie) sont généralement choisis pour les applications où la phase linéaire n’est pas trop importante et où la mémoire est limitée. Ils ont été largement déployés dans l’égalisation audio, le traitement du signal des capteurs biomédicaux, les capteurs intelligents IoT/IIoT et les applications de télécommunication/RF à haut débit.
Avantages
- Faible coût de mise en œuvre: nécessite moins de coefficients et de mémoire que les filtres RIF pour satisfaire un ensemble similaire de spécifications, à savoir la fréquence de coupure et l’atténuation de la bande d’arrêt
- Faible latence: : sconvient aux applications de contrôle en temps réel et aux applications RF à très haut débit en raison du faible nombre de coefficients
- Équivalent analogique: peut être utilisé pour imiter les caractéristiques des filtres analogiques en utilisant des transformations de mappage dans le plan s-z
Inconvénients
- Caractéristiques de phase non linéaires: Les caractéristiques de phase d’un filtre RII sont généralement non linéaires, en particulier à proximité des fréquences de coupure. Des filtres d’égalisation passe-tout peuvent être utilisés afin d’améliorer les caractéristiques de phase de la bande passante
- Analyse plus détaillée : Nécessite plus d’analyse de mise à l’échelle et de débordement numérique lorsqu’il est implémenté en virgule fixe. La structure du filtre de forme directe II est particulièrement sensible aux effets de la quantification, et nécessite une attention particulière lors de la phase de conception
- Stabilité numérique: : Moins stable numériquement que leurs homologues RIF (réponse impulsionnelle finie), en raison des chemins de rétroaction
Filtres RIF
Les filtres RIF (réponse impulsionnelle finie) sont généralement choisis pour les applications où la phase linéaire est importante et où une quantité décente de mémoire et de performance de calcul est disponible. Ils sont largement utilisés dans les applications d’amélioration des signaux audio et biomédicaux. Leur structure entièrement nulle (discutée ci-dessous) garantit qu’ils ne deviennent jamais instables pour n’importe quel type de signal d’entrée, ce qui leur donne un net avantage sur les filtres RII.
Avantages
- Phase linéaire: Les RIF peuvent être facilement conçus pour avoir une phase linéaire. Cela signifie qu’aucune distorsion de phase n’est introduite dans le signal à filtrer, car toutes les fréquences sont décalées dans le temps de la même quantité – ce qui maintient leurs relations harmoniques relatives (c’est-à-dire un retard de groupe et de phase constant). Ce n’est certainement pas le cas avec les filtres RII, qui ont une caractéristique de phase non linéaire
- Stabilité: Comme les filtresRIF n’utilisent pas les valeurs de sortie précédentes pour calculer leur sortie actuelle, c’est-à-dire qu’ils n’ont pas de rétroaction, ils ne peuvent jamais devenir instables pour tout type de signal d’entrée, ce qui leur donne un avantage distinct sur les filtres RII
- Réponse en fréquence arbitraire: : La fonction firarb() fde Parks-McClellan et ASN FilterScript permet la conception d’un RIF avec une réponse en amplitude arbitraire. Cela signifie qu’un RIF peut être personnalisé plus facilement qu’un RII
- Performance à point fixe: les effets de la quantification sont moins sévères que ceux d’un RII
Inconvénients
- Exigences élevées en termes de calcul et de mémoire: Les RIF nécessitent généralement beaucoup plus de coefficients pour obtenir une coupure nette que leurs homologues RII. Il en résulte qu’ils nécessitent beaucoup plus de mémoire et un nombre beaucoup plus élevé d’opérations MAC (multiple and accumulate). Toutefois, les architectures de microcontrôleurs modernes basées sur les cœurs Cortex-M d’Arm incluent désormais un support matériel DSP via SIMD (instruction de signal, données multiples) qui accélère considérablement l’opération de filtrage.
- Latence plus élevée: le nombre plus élevé de coefficients signifie qu’en général, un RIF est moins adapté qu’un RII pour les applications rapides à haut débit. Cela devient problématique pour les applications de contrôle en boucle fermée en temps réel, où un filtre RIF peut avoir un retard de groupe trop important pour atteindre la stabilité de la boucle
- Pas d’équivalent analogique: : à l’aide de la transformation Bilinéaire, appariée en z (s-z mapping), un filtre analogique peut être facilement transformé en un filtre RII équivalent. Cependant, cela n’est pas possible pour un RIF car il n’a pas d’équivalent analogique
Définitions mathématiques
Comme nous l’avons vu dans l’introduction, les noms RII et RIF proviennent des définitions mathématiques de chaque type de filtre, c’est-à-dire qu’un filtre RII est catégorisé par sa réponse impulsionnelle théoriquement infinie,
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)
et un RIF catégorisé par sa réponse impulsionnelle finie,
y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)
\)
Nous allons maintenant analyser successivement les propriétés mathématiques de chaque type de filtre.
Définition du filtre RII
Comme nous l’avons vu plus haut, un filtre RII est catégorisé par sa réponse impulsionnelle théoriquement infinie,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x(n-k) \)
En pratique, il n’est pas possible de calculer la sortie d’un RII à l’aide de cette équation. Par conséquent, l’équation peut être réécrite en termes d’un nombre fini de pôles \(\small p\) et de zéros \(\small q\), comme défini par l’équation de différence linéaire à coefficient constant donnée par:
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
où, \(\small a_k\) et \(\small b_k\) sont les coefficients polynomiaux du dénominateur et du numérateur du filtre, dont les racines sont égales aux pôles et aux zéros du filtre, respectivement. Ainsi, une relation entre l’équation différentielle et la transformée en z (fonction de transfert) peut donc être définie en utilisant la propriété de retard de la transformée en z telle que,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
\)
Comme on le voit, la fonction de transfert est une représentation du filtre dans le domaine fréquentiel. Remarquez également que les pôles agissent sur les données de sortie, et les zéros sur les données d’entrée. Since the poles act on the output data, and affect stability,Puisque les pôles agissent sur les données de sortie et affectent la stabilité, il est essentiel que leurs rayons restent à l’intérieur du cercle unitaire (i.e. <1) pour la stabilité BIBO (bounded input, bounded output). Les rayons des zéros sont moins critiques, car ils n’affectent pas la stabilité du filtre. C’est la principale raison pour laquelle les filtres RIF (réponse impulsionnelle finie) tout-zéro sont toujours stables.
Stabilité BIBO
Un système linéaire invariant dans le temps (LTI) (tel qu’un filtre numérique) est dit stable à entrée bornée et sortie bornée, ou stable BIBO, si chaque entrée bornée donne lieu à une sortie bornée, comme suit
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|%lt\infty \)
Où, \(\small h(k)\) est la réponse impulsionnelle du système LTI. En analysant cette équation, il devrait être clair que le critère de stabilité BIBO ne sera satisfait que si les pôles du système se trouvent à l’intérieur du cercle unitaire, puisque la ROC (région de convergence) du système doit inclure le cercle unitaire. Par conséquent, il suffit de dire qu’un signal d’entrée borné produira toujours un signal de sortie borné si tous les pôles se trouvent à l’intérieur du cercle unitaire.
Les zéros, par contre, ne sont pas contraints par cette exigence et, par conséquent, peuvent se trouver n’importe où sur le plan z, puisqu’ils n’affectent pas directement la stabilité du système. Par conséquent, une analyse de la stabilité du système peut être entreprise en calculant d’abord les racines de la fonction de transfert (c’est-à-dire les racines des polynômes du numérateur et du dénominateur), puis en traçant les pôles et les zéros correspondants sur le plan zéro.
Une situation intéressante se présente si l’un des pôles se trouve sur le cercle unitaire, car le système est dit marginalement stable, puisqu’il n’est ni stable ni instable. Bien que les systèmes marginalement stables ne soient pas stables BIBO, ils ont été exploités par les concepteurs d’oscillateurs numériques, car leur réponse impulsionnelle fournit une méthode simple pour générer des ondes sinusoïdales, qui se sont avérées précieuses dans le domaine des télécommunications.
Filtres RII biquad
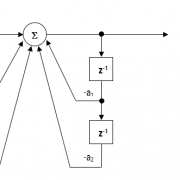
La mise en œuvre du filtre RII dont il est question ici est dite biquad, car elle comporte deux pôles et deux zéros, comme l’illustre la figure 2 ci-dessous. L’implémentation biquad est particulièrement utile pour les implémentations en virgule fixe, car les effets de la quantification et de la stabilité numérique sont minimisés. Cependant, le succès global de toute implémentation biquad dépend de la précision numérique disponible, qui doit être suffisante pour garantir que les pôles quantifiés sont toujours à l’intérieur du cercle unitaire.
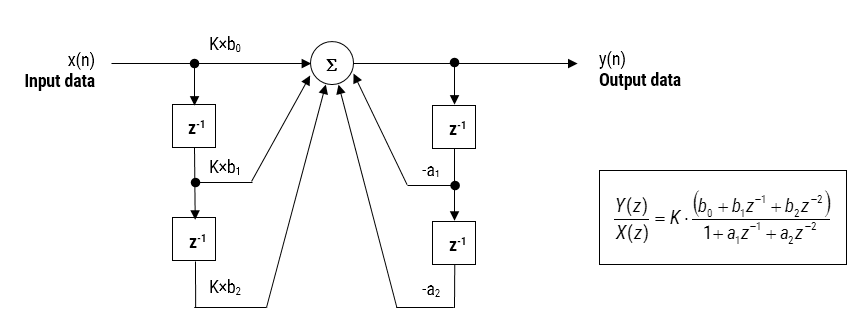
Figure 2 : Réalisation et fonction de transfert d’un filtre RII de forme directe I (biquad)
En analysant la figure 2, on constate que la structure biquad est en fait composée de deux chemins de rétroaction (mis à l’échelle par (scaled by \(\small a_1\) et \(\small a_2\)), tde trois chemins de rétroaction (mis à l’échelle par \(\small b_0, b_1\) et \(\small b_2\)) et d’un gain de section, \(\small K\).Ainsi, l’opération de filtrage de la figure 1 peut être résumée par l’équation récursive simple suivante :
\(\displaystyle y(n)=K\times\Big[b_0 x(n) + b_1 x(n-1) + b_2 x(n-2)\Big] – a_1 y(n-1)-a_2 y(n-2)\)
En analysant l’équation, on remarque que l’implémentation biquad ne nécessite que quatre additions (qui ne requièrent qu’un seul accumulateur) et cinq multiplications, ce qui peut être facilement accommodé sur n’importe quel microcontrôleur Cortex-M. Le gain de section, \(\small K\) , peut également être prémultiplié avec les coefficients de la voie directe avant l’implémentation.
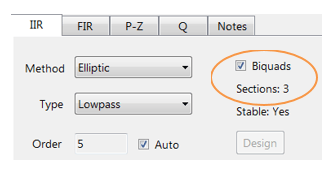
Une collection de filtres Biquad est appelée une cascade Biquad, comme illustré ci-dessous.
Le ASN Filter Designer peut concevoir et implémenter une cascade de jusqu’à 50 biquads (édition professionnelle seulement).
Implémentation en virgule flottante
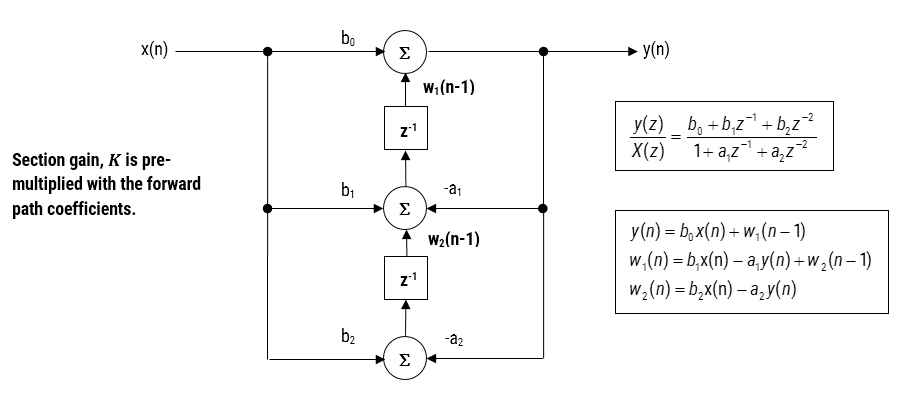
Lors de l’implémentation d’un filtre en virgule flottante (c’est-à-dire en utilisant l’arithmétique de double ou simple précision) les structures Direct Form II sont considérées comme un meilleur choix que la structure Direct Form I. La structure de forme directe II transposée est considérée comme la plus précise numériquement pour une implémentation en virgule flottante, car les effets indésirables de l’amortissement numérique sont minimisés, comme on peut le voir en analysant les équations de différence.
Figure 3 – Structure transposée de forme directe II, fonction de transfert et équations de différence
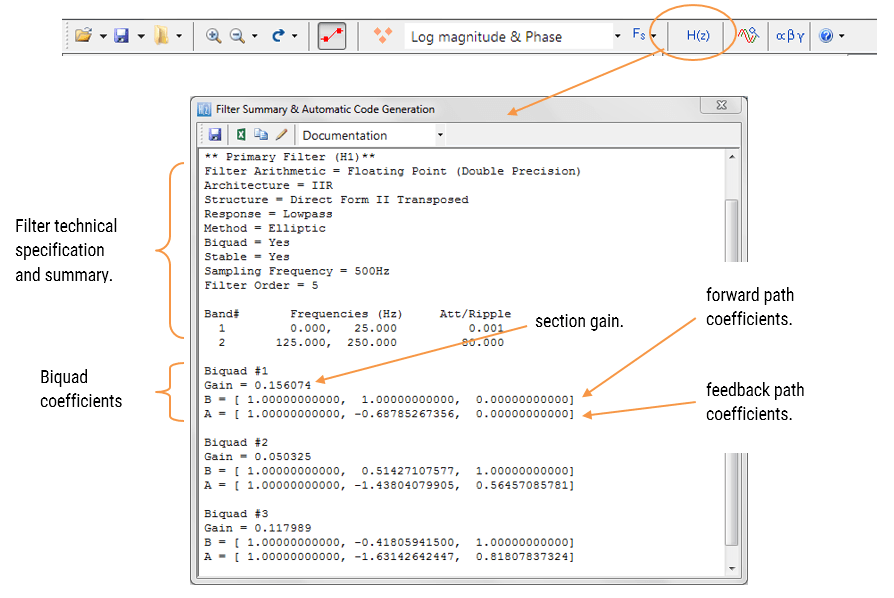
Le résumé du filtre (montré dans la Figure 4) fournit au concepteur une vue d’ensemble détaillée du filtre conçu, y compris un résumé détaillé des spécifications techniques et des coefficients du filtre, qui présente une voie rapide et simple pour documenter votre conception.
Le ASN Filter Designer supporte la conception et l’implémentation des filtres RII à section unique et Biquad (réglage par défaut).
Définition RIF
En retournant l’équation de différence de coefficient constant linéaire du RII, c’est-à-dire
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
Remarquez que lorsque nous mettons les coefficients \(\small a_k\) (c’est-à-dire la rétroaction) à zéro, la définition se réduit à notre définition originale du filtre RIF, ce qui signifie que le calcul RIF est juste basé sur les valeurs d’entrée passées et présentes, à savoir:
y(n)=\sum_{k=0}^{q}b_kx(n-k)
\)
Implémentation
Bien qu’il existe plusieurs implémentations pratiques pour les RIF, la structure de forme directe et son cousin transposé sont peut-être les plus couramment utilisés, et en tant que tels, tous les coefficients de filtre conçus sont destinés à être implémentés dans une structure de forme directe.
La structure de forme directe et l’équation de différence associée sont présentées ci-dessous. La forme directe est préconisée pour la mise en œuvre en virgule fixe en vertu du concept d’accumulateur unique.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)
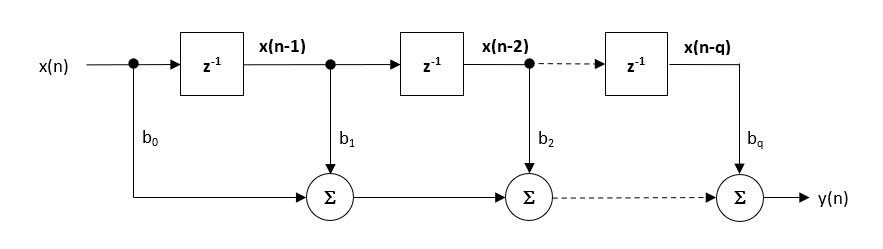
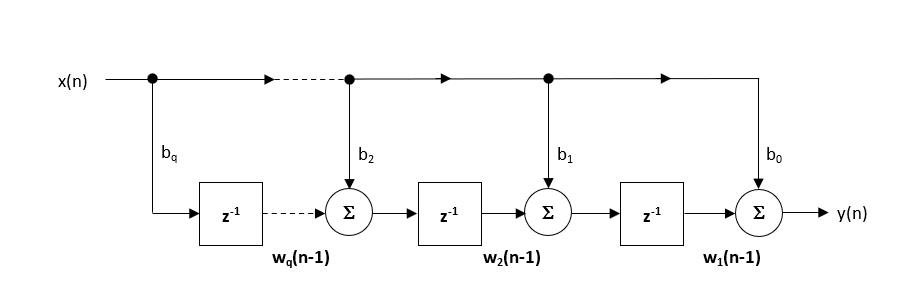
La structure recommandée (par défaut) dans l’ASN Filter Designer est la structure Direct Form Transposed, car elle offre une précision numérique supérieure lors de l’utilisation de l’arithmétique à virgule flottante. Ceci peut être facilement vu en analysant les équations de différence ci-dessous (utilisées pour l’implémentation), car les effets indésirables de l’amortissement numérique sont minimisés, puisque l’addition en virgule flottante est effectuée sur des nombres de magnitude similaire.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
Qu’avons-nous appris ?
Les filtres numériques se répartissent dans les deux catégories suivantes :
- Réponse impulsionnelle infinie (RII)
- Réponse impulsionnelle finie (RIF)
Les filtres RII (Réponse impulsionnelle infinie) sont généralement choisis pour des applications où la phase linéaire n’est pas trop importante et où la mémoire est limitée. Ils ont été largement déployés dans l’égalisation audio, le traitement du signal des capteurs biomédicaux, les capteurs intelligents IoT/IIoT et les applications de télécommunication/RF à haut débit.
Les filtres RIF (réponse impulsionnelle finie) sont généralement choisis pour les applications où la phase linéaire est importante et où une quantité décente de mémoire et de performances de calcul sont disponibles. Ils ont été largement déployés dans les applications d’amélioration des signaux audio et biomédicaux.
ASN Filter Designer fournit aux ingénieurs tout ce dont ils ont besoin pour concevoir, expérimenter et déployer des filtres numériques complexes RII et RIF pour une variété d’applications de mesure de capteurs. Ces avantages couplés avec la documentation automatique et la fonctionnalité de génération de code permettent aux ingénieurs de concevoir et valider un filtre numérique RII/RIF en quelques minutes plutôt qu’en quelques heures.







Leave a Reply
Want to join the discussion?Feel free to contribute!