Farrow Verzögerungsfilter

Bei der Signalverarbeitung besteht manchmal die Notwendigkeit, die Abtastzeitpunkte eines Signals um einen Bruchteil einer Abtastung zu verschieben oder fein abzustimmen. Für diese Aufgabe wird in der Regel ein FIR-Farrow-Verzögerungsfilter verwendet, das mit einer herkömmlichen ganzzahligen Verzögerungsleitung kombiniert werden kann, um eine universelle Verzögerungsleitung mit gebrochener Länge zu erhalten.

Eine fraktionale Verzögerung auf der Grundlage einer FIR-Farrow-Struktur kann wie folgt definiert werden:

\(H(z)=(1-\alpha)+\alpha z^{-1}; \; 0 \leq \alpha \leq 1 \)

Daraus ergibt sich eine fraktionierte lineare Verzögerung von \(\alpha\) zwischen 0 und 1 Samples. Ein universellerer Baustein kann jedoch durch die Kombination der Farrow-Verzögerungsstruktur mit einer ganzzahligen Verzögerung, \(\Delta\) erreicht werden.

\(H(z)=(1-\alpha) z^{-\Delta}+\alpha z^{-(\Delta+1)}\)

Die nachstehende Grafik zeigt die Spektren von Betrag (blau) und Phase (lila) für \(\Delta=9, \, \alpha=0.52\). Wie man sieht, führt das fraktionierte Verzögerungselement zu einem nicht flachen Betragsspektrum bei höheren Frequenzen.

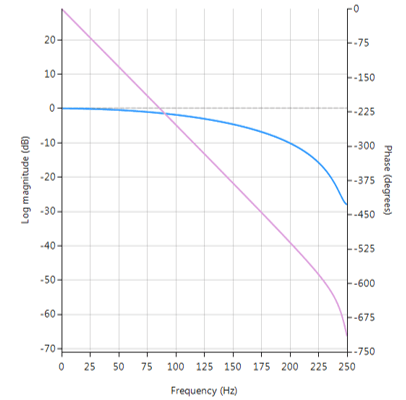
Frequenzgang des Farrow-Verzögerungsfilters

Implementierung

Ein Farrow-Delay-Filter kann in ASN FilterScript wie folgt implementiert werden:
[code language=”java”]
ClearH1; // clear primary filter from cascade

interface alpha = {0,1,0.02,.5}; // fractional delay
interface D = {1,30,1,10}; // integer delay

Main()
Num = {zeros(D),1-alpha,alpha}; // numerator coefficients
Den = {1}; // denominator coefficient
Gain = 1/sum(Num); // normalise gain at DC
[/code]