FIR arbitrary magnitude response filter

Syntax
Hd = firarb(Order,Amplitude,Frequencies,Window,DFormat)

Description
Designs an FIR window based filter with an arbitrary magnitude response.

Order: may be specified up to 499 (professional) and up to 128 (educational) edition.

Amplitude: a vector of the magnitude specification in dB.

Frequencies: a vector of the frequency specification. The first element must be 0 and the last element equal to Nyquist – see below.

Window: The firarb method supports the following window functions: rectangular, blackman, blackmanharris, hamming, hanning, flattop and Chebyshev.

Hd: the firarb method designs an FIR filter based on the entered specifications and places the transfer function (i.e. numerator and gain) into a digital filter object, Hd. The digital filter object can then be combined with other methods if so required. For a digital filter object, Hd, calling getnum(Hd) and getgain(Hd) will extract the numerator and gain coefficients respectively – see below.

DFormat: allows you to specify the display format of resulting digital filter object.

symbolic Display a symbolic representation of the filter object. If the order > 10, the symbolic display option will be overridden and set to numeric.
numeric Display a matrix representation of the filter object
void Create a filter object, but do not display output

Example

ClearH1; // clear primary filter from cascade
ShowH2DM;

interface L = {10,400,10,50};

Main()

A=series(0,-1,-40);
F=series(10,90/(length(A)-1),100);
A={0,A,-100,-100}; // specify arb response
F={0,F,101,fs/2}; //

Hd=firarb(L,A,F,"hanning","numeric");

Num=getnum(Hd);
Den={1};
Gain=getgain(Hd);

Results

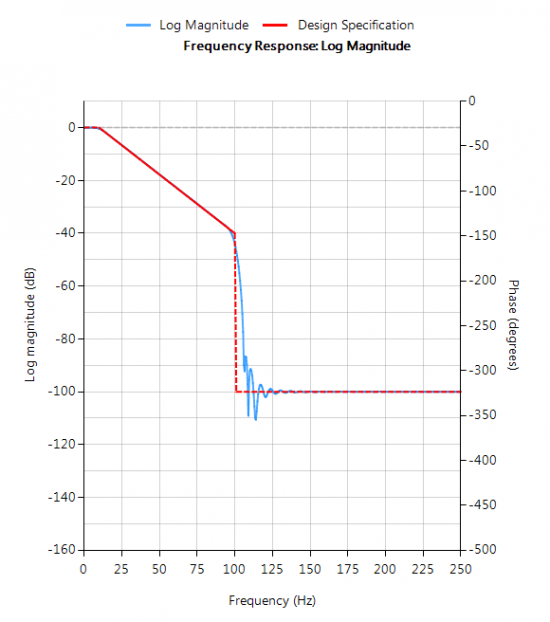
Running the script shown above, we obtain the following plots (with and without the design markers). Where, it can be seen that the design specifications have been met.

fir arbitrary magnitude filter

fir arb filter

See also:

movaver / firwin / firarb / firkaiser / firgauss / firlp2notch / savgolay