FIR-Filter (Finite Impulse Response) sind für eine Vielzahl von Sensor-Signalverarbeitungsanwendungen nützlich, einschließlich Audio- und biomedizinischer Signalverarbeitung. Obwohl es mehrere praktische FIR-Implementierungen gibt, bietet die Direct Form Transposed-Struktur die beste numerische Genauigkeit für die Fließkomma-Implementierung. Wenn jedoch eine Festkomma-Implementierung auf einem Mikrocontroller in Betracht gezogen wird, gilt die Direct-Form-Struktur aufgrund ihres großen Akkumulators, der alle Zwischenüberläufe aufnehmen kann, als beste Wahl.
Diese Application Note befasst sich speziell mit dem Entwurf und der Implementierung von FIR-Filtern auf einem Cortex-M-basierten Mikrocontroller mit dem ASN Filter Designer sowohl für Fließkomma- als auch für Festkomma-Anwendungen über das Arm CMSIS-DSP Software Framework. Es werden auch Details (einschließlich eines Arm-Referenz-Softwarepakets) zur Implementierung des FIR-Filters in Arm/Keils MDK-Industriestandard-Cortex-M-Mikrocontroller-Entwicklungskit gegeben.
Einführung
ASN Filter Designer bietet Ingenieuren eine leistungsstarke DSP-Experimentierplattform, die den Entwurf, die Erprobung und den Einsatz komplexer digitaler FIR-Filterdesigns für eine Vielzahl von Sensormessanwendungen ermöglicht. Die fortschrittliche Funktionalität des Tools umfasst einen grafikbasierten Echtzeit-Filterdesigner, mehrere Filterblöcke, verschiedene mathematische E/A-Blöcke, symbolische Live-Mathe-Skripte und Echtzeit-Signalanalyse (über einen integrierten Signalanalysator). Diese Vorteile in Verbindung mit der automatischen Dokumentation und Code-Generierung ermöglichen es den Ingenieuren, einen digitalen Filter innerhalb von Minuten statt Stunden zu entwerfen und zu validieren.
Das Arm CMSIS-DSP (Cortex Microcontroller Software Interface Standard) Software-Framework ist eine reichhaltige Sammlung von über sechzig DSP-Funktionen (einschließlich verschiedener mathematischer Funktionen wie Sinus und Kosinus, IIR/FIR-Filterfunktionen, komplexer mathematischer Funktionen und Datentypen), die von Arm entwickelt und für die Cortex-M-Prozessorkerne optimiert wurden.

Das Framework macht ausgiebig Gebrauch von hoch optimierten SIMD-Befehlen (Single Instruction, Multiple Data), die mehrere identische Operationen in einem einzigen Befehlszyklus ausführen. Die SIMD-Befehle (sofern sie vom Kern unterstützt werden) in Verbindung mit anderen Optimierungen ermöglichen es Ingenieuren, schnell und einfach hoch optimierte Signalverarbeitungsanwendungen für Cortex-M-basierte Mikrocontroller zu erstellen.
Der ASN Filter Designer unterstützt das CMSIS-DSP Software-Framework vollständig, indem er über seine Code-Generierungs-Engine automatisch optimierten C-Code auf Basis der DSP-Funktionen des Frameworks erzeugt.
Entwurf von FIR-Filtern mit dem ASN Filter Designer
Der ASN Filter Designer bietet Ingenieuren eine einfach zu bedienende, intuitive grafische Entwicklungsplattform für den Entwurf digitaler FIR-Filter. Das Echtzeit-Entwurfsparadigma des Tools nutzt grafische Entwurfsmarkierungen, die es den Entwicklern ermöglichen, ihre Anforderungen an den Frequenzgang in Echtzeit zu zeichnen und zu ändern, während das Tool automatisch die genauen Spezifikationen für sie ausfüllt.
Betrachten Sie den Entwurf der folgenden technischen Spezifikation:
| Fs: | 500Hz |
| Durchlassband-Frequenz: | 0-25Hz |
| Typ: | Lowpass |
| Methode: | Parks-McClellan |
| Dämpfung des Sperrbereichs @ 125Hz: | ≥ 80 dB |
| Durchlassband-Welligkeit: | < 0.01dB |
| Ordnung: | So klein wie möglich |
Durch die grafische Eingabe der Spezifikationen in den ASN Filter Designer und die Feinabstimmung der Design-Marker-Positionen entwirft das Tool automatisch das Filter, wählt automatisch die erforderliche Filterordnung und produziert im Wesentlichen automatisch die exakte technische Spezifikation des Filters!
Der Frequenzgang eines Filters, das die Spezifikation erfüllt, ist unten dargestellt:
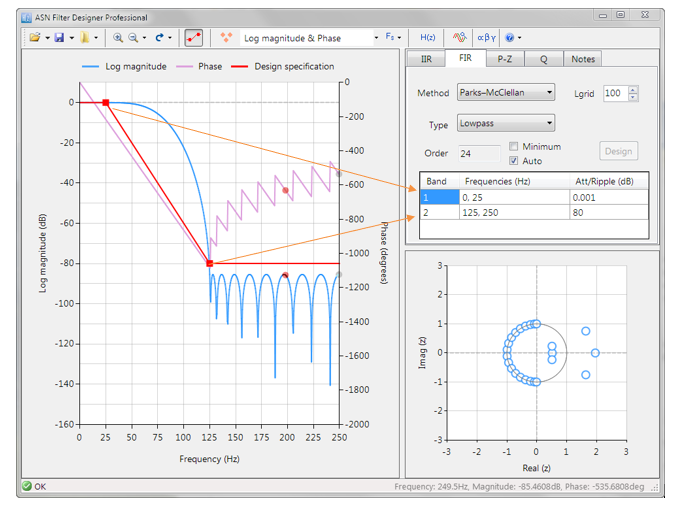
Dieser Tiefpassfilter bildet die Grundlage für die hier geführte Diskussion.
Parks-McClellan-Algorithmus
Der Parks-McClellan-Algorithmus ist ein iterativer Algorithmus zur Ermittlung des optimalen Tschebyscheff-FIR-Filters. Der Algorithmus verwendet eine indirekte Methode zur Ermittlung der optimalen Filterkoeffizienten, die im Vergleich zu anderen FIR-Entwurfsmethoden ein gewisses Maß an Flexibilität bietet, da jedes Band individuell angepasst werden kann, um den Anforderungen des Designers zu entsprechen.
Die primäre FIR-Filter-Designer-UI implementiert den Parks-McClellan-Algorithmus und ermöglicht den Entwurf der folgenden Filtertypen:
| Filtertypen | Beschreibung |
| Tiefpass | Entwirft einen Tiefpassfilter |
| Hochpass | Entwirft einen Hochpassfilter |
| Bandpass | Entwirft ein Bandpassfilter |
| Bandsperre | Entwirft ein Bandsperrfilter |
| Multiband | Entwirft ein Multiband-Filter mit beliebigem Frequenzgang |
| Hilbert-Transformator | Entwirft ein Allpassfilter mit einer Phasenverschiebung von -90 Grad |
| Differentiator | Entwirft einen Filter mit +20dB/Dekade Steigung und +90 Grad Phasenverschiebung |
| Doppelter Differenzierer | Entwirft einen Filter mit einer Steigung von +40 dB/Dekade und einer Phasenverschiebung von +90 Grad |
| Integrator | Entwirft einen Filter mit einer Steigung von -20 dB/Dekade und einer Phasenverschiebung von -90 Grad |
| Doppelintegrator | Designs a filter with -40dB/decade slope and a -90 degree phase shift. |
Diese zehn Filtertypen bieten Entwicklern eine große Flexibilität für eine Vielzahl von IoT-Anwendungen. Die Designanforderungen können einfach durch die Verwendung der Designmarker spezifiziert werden. In allen Fällen berechnet das Tool automatisch die erforderliche Filterreihenfolge, um die Spezifikation des Designers zu erfüllen.

Der Parks-McClellan-Algorithmus ist eine optimale Tschebyscheff-FIR-Entwurfsmethode. Allerdings konvergiert der Algorithmus bei einigen Spezifikationen möglicherweise nicht. In solchen Fällen hilft es im Allgemeinen, den Abstand zwischen den Entwurfsmarkierungsbändern zu vergrößern.
Andere FIR-Entwurfsmethoden
Designer, die mit anderen Arten von FIR-Entwurfsmethoden experimentieren möchten, können die symbolische Live-Mathe-Skriptsprache ASN FilterScript verwenden. Die Skriptsprache unterstützt über 65 wissenschaftliche Befehle und bietet Entwicklern eine vertraute und leistungsstarke Programmiersprache, die es ihnen gleichzeitig ermöglicht, komplexe symbolische mathematische Ausdrücke zu implementieren. Die folgenden Funktionen werden unterstützt:
| Funktion | Beschreibung |
| movaver | Moving average FIR filter design: Entwurf eines FIR-Filters mit gleitendem Mittelwert |
| firwin | FIR filter Window method: FIR-Filterentwurf auf der Grundlage der Fenstermethode |
| firarb | Entwirft ein FIR-Filter auf Basis der Fenstermethode mit beliebigem Amplitudengang |
| firkaiser | Entwurf eines FIR-Filters nach der Kaiser-Fenstermethode |
| firgauss | Entwurf eines FIR Gaußschen Tiefpassfilters |
| savgolay | Entwirft ein FIR Savitzky-Golay Tiefpass-Glättungsfilter |
Weitere Details finden Sie im ASN FilterScript Reference Guide.
Alle Filter, die in ASN FilterScript entworfen werden, werden unter Verwendung von Arithmetik mit doppelter Genauigkeit in der H2-Filter-Sandbox entworfen. Ein H2-Filter muss für den Einsatz in einen H1-(Primär-)Filter umgewandelt werden.
Dies kann einfach über das Optionsmenü P-Z erreicht werden:
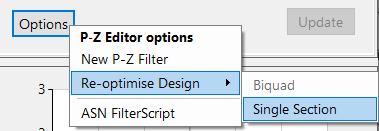
Die Re-Optimierungsmethode analysiert automatisch den H2-Filter und wandelt ihn in einen H1-Filter um.
Fließkomma-Implementierung
Bei der Implementierung eines Filters in Fließkomma (‘floating point’; d.h. unter Verwendung von Arithmetik mit doppelter oder einfacher Genauigkeit) gilt die Struktur Direct Form Transposed als die numerisch genaueste. Dies lässt sich leicht erkennen, wenn man die nachstehenden (für die Implementierung verwendeten) Differenzgleichungen analysiert, da die unerwünschten Auswirkungen der numerischen Übersättigung minimiert werden, da die Fließkommaaddition auf Zahlen ähnlicher Größenordnung durchgeführt wird.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
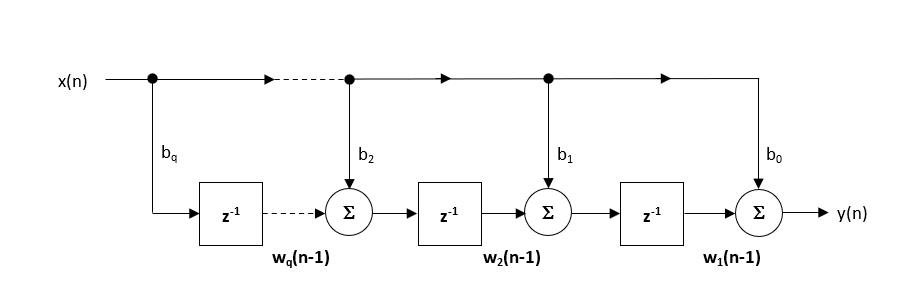
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
Die Quantisierungs- und Filterstruktureinstellungen, die zur Implementierung der FIR verwendet werden, finden Sie auf der Registerkarte Q (wie unten dargestellt).

Obwohl die Direct Form Transposed-Struktur für die Fließkomma-Implementierung am effizientesten ist, unterstützt die Arm CMSIS-DSP-Bibliothek derzeit nicht die Direct Form Transposed-Struktur für FIR-Filter. Es wird nur die Direct Form Struktur unterstützt.
Wenn Sie die Arithmetic auf Single Precision und Structure auf Direct Form einstellen und auf die Schaltfläche Apply klicken, wird die hier betrachtete FIR für das CMSIS-DSP Software Framework konfiguriert.
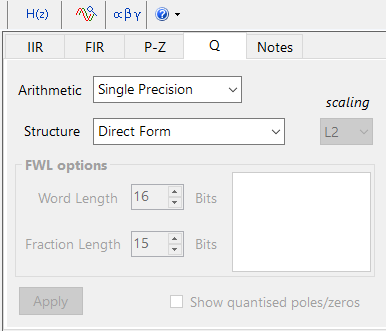

Die optimierten Funktionen innerhalb des Arm CMSIS-DSP Frameworks unterstützen derzeit nur Single Precision Arithmetik.
Unterstützung für Double Precision und die Direct Form Transposed-Struktur wird in zukünftigen Versionen hinzugefügt werden.
Festkomma-Implementierung
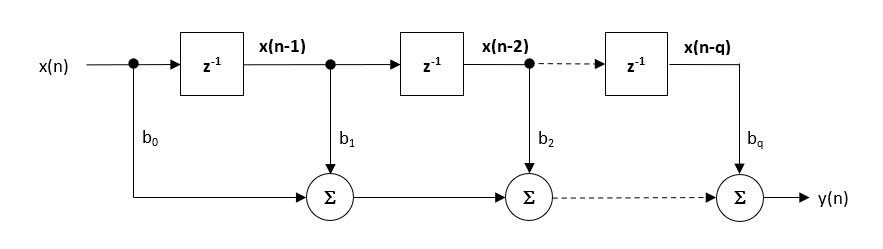
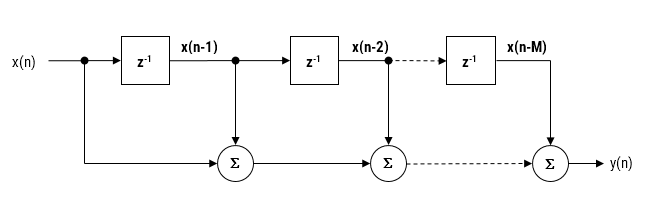
Bei der Implementierung eines Filters mit Festkomma-Arithmetik wird die Direct-Form-Struktur aufgrund ihres großen Akkumulators, der alle Zwischenüberläufe aufnimmt, als die beste Wahl angesehen. Die Direct-Form-Struktur und die zugehörige Differenzengleichung sind im Folgenden dargestellt.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)
Das CMSIS-DSP-Framework unterstützt nur die Quantisierung der Koeffizienten Q7, Q15 und Q31. Die Optionen können einfach über die Registerkarte Q für die Quantisierung angegeben werden, wie unten gezeigt:
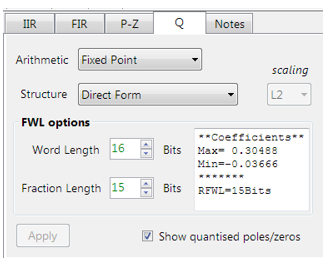
Die eingebauten Analysen des Tools (in der Textbox) sollen dem Designer helfen, die am besten geeigneten Quantisierungseinstellungen zu wählen.
Wie links zu sehen ist, hat das Tool eine RFWL (empfohlene Fraktionslänge) von 15 Bits (Q15) für die Koeffizienten empfohlen, was den Anforderungen entspricht.
Die Struktur Direkte Form wird der Struktur Direkte Form Transponiert vorgezogen, da ein einziger Akkumulator (40 Bit) verwendet werden kann. Der automatische Code-Generator des Tools nutzt die 64-Bit-Akkumulatoren-Funktionen von CMSIS-DSP, so dass der endgültige C-Code, der auf einem Cortex-M-Baustein eingesetzt wird, nicht überläuft.
Bereitstellung von Arm CMSIS-DSP-konformem Code
Die automatische Code-Generierungs-Engine des ASN Filter Designers erleichtert den Export eines entworfenen Filters auf Cortex-M Arm-basierte Prozessoren über das Arm CMSIS-DSP Software-Framework. Die integrierten Analyse- und Hilfefunktionen des Tools unterstützen den Designer bei der erfolgreichen Konfiguration des Designs für den Einsatz.
Wählen Sie das Arm CMSIS-DSP-Framework aus der Auswahlbox im Filterübersichtsfenster aus:
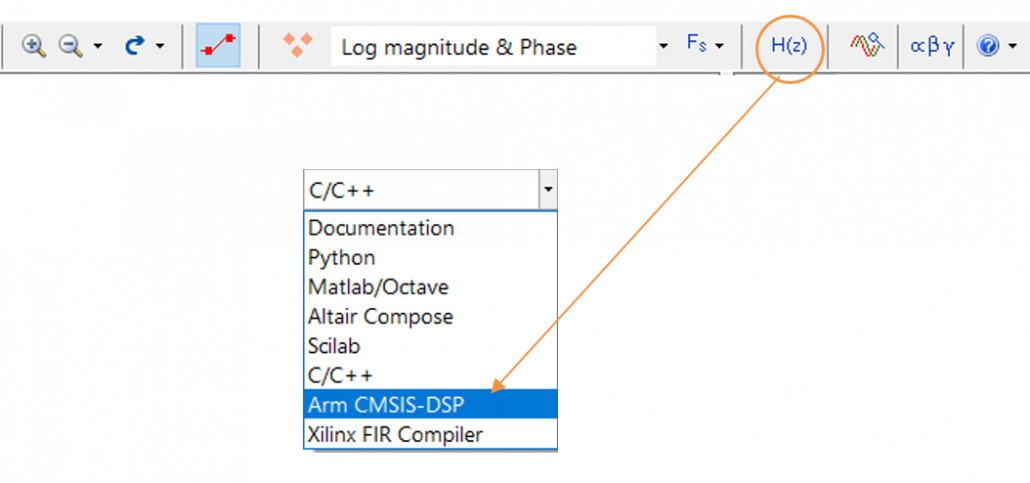
Der automatisch generierte C-Code auf Basis des Arm CMSIS-DSP-Frameworks für die direkte Implementierung auf einem Arm-basierten Cortex-M-Prozessor ist unten dargestellt:
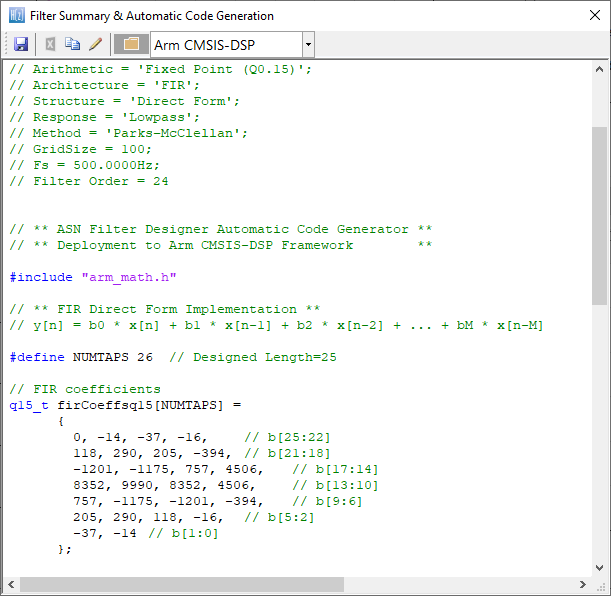
Dieser Code kann direkt in jedem Cortex-M-basierten Entwicklungsprojekt verwendet werden.
Arm Keil MDK (uVision)
Wie bereits erwähnt, kann der vom Arm CMSIS DSP Code-Generator erzeugte Code direkt in jedem Cortex-M-basierten Entwicklungsprojekt-Tooling verwendet werden, wie z.B. Arm Keils Industriestandard uVision MDK (Micro-Controller Development Kit).
Das folgende Arm-Softwarepaket ist auf Keils Website verfügbar, um diesen Code direkt mit Keil uVision MDK zu verwenden.


Leave a Reply
Want to join the discussion?Feel free to contribute!