Kammfilter: Unterdrückung von Oberschwingungen im Stromnetz und CIC

Kammfilter werden als Netzfilter (50/60 Hz) zur Auslöschung von Oberwellen in Audioanwendungen eingesetzt und bilden die Grundlage für sogenannte CIC-Filter (Cascaded Integrator-Comb), die für Anti-Aliasing bei der Dezimierung (Verringerung der Abtastrate) und Anti-Imaging bei Interpolationsanwendungen (Erhöhung der Abtastrate) verwendet werden.

Der Frequenzgang eines Kammfilters besteht aus einer Reihe von regelmäßig beabstandeten Mulden, die das Aussehen eines Kamms ergeben. Wie in der Abbildung unten zu sehen ist, erscheint der Abstand der einzelnen Senken entweder bei ungeraden oder geraden Oberwellen der gewünschten Grundfrequenz.

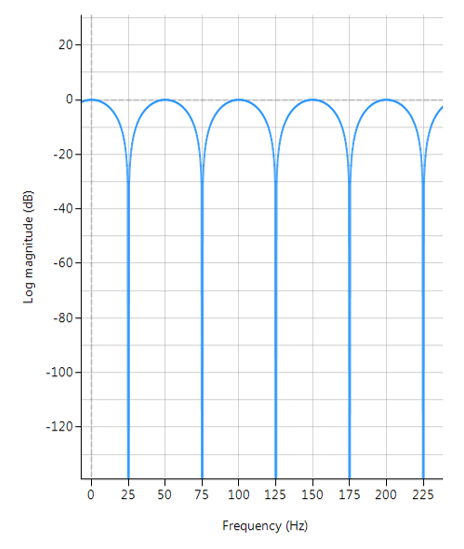Frequenzgang eines typischen FIR-Kammfilters (Auslöschung ungerader Harmonischer):
\(f_s=500Hz\), \(f_c=25Hz\), \(L=10\) und \(\alpha=1\)

Ein FIR-Kammfilter kann durch die folgende Übertragungsfunktion beschrieben werden:

\(H(z)=1+\alpha z^{-L}\)
\(\Rightarrow Y(z)=X(z)\left[1+\alpha z^{-L}\right]\)

Offensichtlich ist das Kammfilter einfach ein gewichtetes verzögertes Replikat seiner selbst, spezifiziert durch \(L\). Durch inverse z-Transformationen erhalten wir die für die Implementierung benötigte Differenzengleichung,

\(y(n)=x(n)+\alpha x(n-L)\)

wobei \(\alpha\) zur Einstellung der Q (Bandbreite) der Kerbe verwendet wird und entweder positiv oder negativ sein kann, je nachdem, welche Art von Frequenzgang erforderlich ist. Um dies zu verdeutlichen: Negative Werte von \(\alpha\) haben ihren ersten Tiefpunkt bei DC und ihren zweiten Tiefpunkt bei der Grundfrequenz. Es ist klar, dass diese Art von Kammfilter verwendet werden kann, um DC-Komponenten aus einer gemessenen Wellenform zu entfernen, falls dies erforderlich ist. Alle nachfolgenden Tiefpunkte erscheinen bei geraden Harmonischen bis einschließlich der Nyquist-Frequenz.

Positive Werte von \(\alpha\) hingegen haben nur Mulden bei der Grundfrequenz und den ungeraden Harmonischen und können daher nicht zur Entfernung von Gleichstromanteilen verwendet werden.

Anwendung zur Powerline-Entstörung

Die Wirksamkeit des Kammfilters ist abhängig von der Abtastfrequenz \(f_s\), da \(L\) nur auf ganzzahlige Werte beschränkt ist. Außerdem ist eine Beziehung zwischen \(f_s\), da \(L\) und vom Vorzeichen von \(\alpha\) abhängig. Daher werden für die Zwecke der in dieser Diskussion betrachteten Anwendung zur Netzentstörung nur positive Werte von berücksichtigt, da wir nur ungerade Oberwellen auslöschen müssen.

Eine einfache Beziehung zur Bestimmung von \(L\) lässt sich für positive Werte von \(\alpha\) wie folgt zusammenfassen:

\(L=ceil\left( \large{\frac{f_s}{2f_c}}\right)\)

wobei \(f_c\) der gewünschte Mittelpunkt der Kerbgrundfrequenz ist. Basierend auf diesem Ausdruck können wir die Abtastfrequenz neu berechnen, so dass \(f_c\) ein echtes Vielfaches von \(f_s\) ist

\(f_{snew}=2f_c L\)

Beispiel für ein Kammfilter

Für das hier betrachtete Beispiel, d. h. \(fs=500Hz\) und \(fc=25Hz\), erhalten wir \(L=10\). Bei \(f_c=60Hz\) bräuchten wir jedoch \(L=5\), bzw. eine neue Abtastrate von \(600Hz\), wobei interessant ist, dass auch \(f_s=480Hz\) für \(L=4\) ausreichen würde.

Implementierung

Ein FIR-Kammfilter kann in ASN FilterScript wie folgt implementiert werden:
[code language=”java”]
ClearH1; // clear primary filter from cascade
interface L = {4,20,1,5}; // delay
interface alpha = {-1,1,0.01,1};

Main()
Num = {1,zeros(L-1),alpha}; // numerator coefficients
Den = {1};
Gain = 1/sum(abs(Num));
[/code]