Aktualisieren älterer Designs basierend auf analogen Filtern
Analoge Filter gibt es seit den Anfängen der Elektronik. Angefangen von einfachen Induktor-Kondensator-Netzwerken bis hin zu fortschrittlichen aktiven Filtern mit Operationsverstärkern. Daher gibt es eine umfangreiche Sammlung von bewährter Legacy-Filterdesigns für eine breite Palette von Sensormessanwendungen. Mit den Leistungsanforderungen moderner IoT (Internet of Things) -Sensormessanwendungen und niedrigerer Produktkosten werden jedoch digitale Filter, die in den Applikationscode des Mikrocontrollers integriert sind, zur Norm. Wie können wir das Beste aus beiden Welten erhalten??
Anstatt das Rad neu zu erfinden, können Produktdesigner eine bestehende analoge Filterübertragungsfunktion nehmen, sie in eine digitale Form umwandeln (über eine Transformation) und sie als digitalen Filter in einem Mikrocontroller oder DSP (digitaler Signalprozessor) implementieren. Obwohl es Analog-Digital-Transformationen schon seit Jahrzehnten gibt, war die Verfügbarkeit von DSP-Design-Tools für die Optimierung des “transformierten digitalen Filters” etwas begrenzt, was den Design- und Validierungsprozess behinderte.
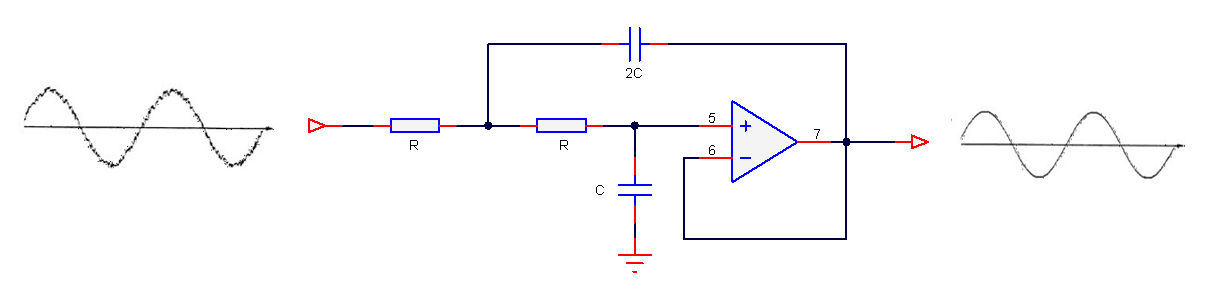
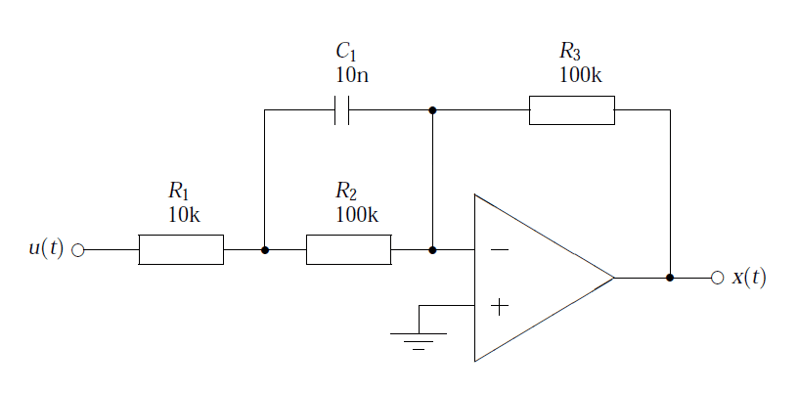
Ein analoges Tiefpassfilter 2. Ordnung ist unten abgebildet, und in seiner einfachsten Form sind nur 5 Komponenten zum Aufbau des Filters erforderlich, was einfach klingt. Oder?
Die Vorteile
Der offensichtlichste Vorteil ist, dass analoge Filter eine hervorragende Auflösung haben, da es keine “Anzahl von Bits” zu berücksichtigen gibt. Analoge Filter haben gute EMV-Eigenschaften (elektromagnetische Verträglichkeit), da es kein takterzeugendes Rauschen gibt. Es gibt keine Aliasing-Effekte, was sicherlich für die einfacheren Operationsverstärker gilt, die keine ausgefallenen Chopping- oder Auto-Kalibrierungsschaltungen eingebaut haben, und analoge Designs können billig sein, was für kostensensitive Anwendungen großartig ist.
Klingt gut, aber was ist die schlechte Nachricht?
Analoge Filter haben einige signifikante Nachteile, die die Filterleistung beeinflussen, wie z. B. die Alterung der Komponenten, Temperaturdrift und Komponententoleranz. Außerdem erfordert eine gute Leistung gute Fähigkeiten im Analogdesign und ein gutes PCB-Layout (Printed Circuit Board), was auf dem heutigen Qualifikationsmarkt schwer zu finden ist.
Diese Nachteile machen digitale Filter viel attraktiver für moderne Anwendungen, die eine hohe Wiederholbarkeit der Eigenschaften erfordern. Zum Beispiel: Nehmen wir an, Sie wollen nach der Optimierung Ihres Filterdesigns 1000 Messmodule herstellen. Mit einer digitalen Lösung können Sie sicher sein, dass die Leistung Ihres Filters in allen Modulen identisch ist. Bei einer analogen Lösung ist dies sicherlich nicht der Fall, da Komponententoleranz, Komponentenalterung und Temperaturdrift dazu führen, dass das Filter jedes Moduls seine eigenen Eigenschaften hat. Außerdem bleibt der Frequenzgang eines analogen Filters fest, d.h. ein Butterworth-Filter ist immer ein Butterworth-Filter – jede Änderung des Frequenzgangs würde einen physischen Austausch von Komponenten auf der Leiterplatte erfordern – nicht ideal!
Digitale Filter sind adaptiv und flexibel. Wir können ein Filter mit einem beliebigen Frequenzgang entwerfen und implementieren, es einsetzen und dann die Filterkoeffizienten aktualisieren, ohne etwas auf der Leiterplatte zu ändern! Es ist auch einfach, digitale Filter mit linearer Phase und sehr niedrigen Abtastfrequenzen zu entwerfen – zwei Dinge, die bei analogen Filtern schwierig sind.
Laplace zu diskreten/digitalen Transformationen
Bei den drei hier besprochenen Methoden geht es im Wesentlichen darum, eine (analoge) Laplace-Übertragungsfunktion, \(H(s)\), in eine diskrete Übertragungsfunktion, \(H(z)\), zu transformieren. So dass ein bewährtes analoges Filter, das bereits in einem Design verwendet wird, auf einem Mikrocontroller oder DSP implementiert werden kann.
Eine Auswahl einiger nützlicher Laplace-zu-z-Transformationen finden Sie in der folgenden Tabelle:
\(
\begin{array}{ccc}\hline
H(s) &\longleftrightarrow & H(z) \\ \hline
1 &\longleftrightarrow & 1 \\
\frac{\displaystyle1}{\displaystyle s}
&\longleftrightarrow& \frac{\displaystyle 1}{\displaystyle 1-z^{\scriptstyle -1}}\\
\frac{\displaystyle 1}{\displaystyle s^{\scriptstyle 2}} &\longleftrightarrow& \frac{\displaystyle
Tz^{\scriptstyle-1}}{\displaystyle (1-z^{\scriptstyle -1})^2}\\
\frac{\displaystyle 1}{\displaystyle s+a}
&\longleftrightarrow&
\frac{\displaystyle 1}{\displaystyle 1-e^{-aT}z^{-1}}\\
\frac{\displaystyle 1}{\displaystyle (s+a)^2}
&\longleftrightarrow& \frac{\displaystyle z^{-1}(1-e^{-aT})}{\displaystyle a(1-z^{-1})(1-e^{-aT}z^{-1})}\\\hline
\end{array}
\)
A table of useful Laplace and z-transforms
Die bilineare z-Transformation (BZT)
Die Bilineare z-Transformation (BZT) wandelt einfach eine analoge Übertragungsfunktion \(H(s)\) in eine diskrete Übertragungsfunktion \(H(z)\) um, indem alle \(s\) -Terme durch die folgenden ersetzt werden:
\(\displaystyle
s=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} \label{bzt}\)
Dabei ist \(T\) die Abtastperiode des diskreten Systems. Ersetzt man jedoch \(s=j\Omega\) und \(z=e^{jwT}\) in die BZT-Gleichung ein und vereinfacht, stellt man fest, dass es tatsächlich eine nichtlineare Beziehung zwischen den analogen \(\Omega\)– und diskreten \(w\)-Frequenzen gibt. Diese Beziehung ist unten gezeigt und ist auf die Nichtlinearität der Arkustangensfunktion zurückzuführen.
\(\displaystyle
\omega=2\tan^{-1}\left(\frac{\Omega T}{2}\right)
\label{bzt_warp_def1}
\)
Bei der Analyse der Gleichung ist zu erkennen, dass die gleichmäßig verteilten analogen Frequenzen im Bereich \(-\infty<\Omega<\infty\) im Frequenzbereich \(-\pi<w<\pi\) im diskreten Bereich nichtlinear komprimiert sind. Diese Beziehung wird als Frequenzverzerrung bezeichnet und kann durch eine Vorverzerrung der analogen Frequenzen kompensiert werden:
\(\displaystyle
\Omega_c=\frac{2}{T}\tan\left(\frac{\Omega_d T}{2}\right)
\label{bzt_warp_def2}
\)
Dabei ist \(\displaystyle\Omega_c\) die kompensierte oder vorgewölbte analoge Frequenz und \(\displaystyle\Omega_d\) die gewünschte analoge Frequenz.
Der ASN FilterScript-Befehl \(\texttt{bilinear}\) kann verwendet werden, um eine Laplace-Übertragungsfunktion in ihr diskretes Äquivalent unter Verwendung der BZT-Transformation umzuwandeln. Ein Beispiel ist unten angegeben.
Die impulsinvariante Transformation
Die zweite Transformation wird als impulsinvariante Transformation (IIT) bezeichnet, da die Pole der Laplace-Übertragungsfunktion in ihre diskreten Äquivalente umgewandelt werden, so dass die diskrete Impulsantwort \(h(n)\) identisch mit einer regelmäßig abgetasteten Darstellung der analogen Impulsantwort ist (d. h. \(h(n)=h(nT)\), wobei \(T\) die Abtastrate und \(t=nT\))ist). Die IIT ist ein wesentlich aufwändigeres Transformationstechnik als die BZT, da die Laplace-Übertragungsfunktion vor der Anwendung der Transformation zunächst mit partiellen Brüchen erweitert werden muss.
Das Transformationsverfahren ist wie folgt definiert:
\(\displaystyle
\frac{K}{s+a} \quad\longrightarrow\quad
\frac{K}{1-e^{-aT}z^{-1}} \label{iit_def}
\)
Diese Methode leidet unter mehreren Einschränkungen, da sie die Transformation von Nullen oder einzelnen konstanten Termen (nach der Expansion) nicht zulässt und eine hohe Abtastrate haben muss, um die Effekte des spektralen Aliasing zu überwinden. In der Tat behindern die Effekte des Aliasing diese Methode erheblich, so dass die Methode nur verwendet werden sollte, wenn die Anforderung besteht, die Impulsantwort der analogen Übertragungsfunktion anzupassen, da das resultierende diskrete Modell ein anderes Betrags- und Phasenspektrum (Frequenzgang) als das des ursprünglichen analogen Systems haben kann. Folglich ist die impulsinvariante Methode für die Modellierung von Hochpassfiltern ungeeignet und daher auf die Modellierung von Tiefpass- oder Bandpassfiltern beschränkt.
Aufgrund der oben genannten Einschränkungen der IIT-Methode wird sie derzeit in ASN Filterscript nicht unterstützt.
Die Matched-z-Transformation
Ein weiteres Analogon zur diskreten Modellierungstechnik ist die Matched-Z-Transformation. Wie der Name schon sagt, wandelt die Transformation die Pole und Nullstellen aus der analogen Übertragungsfunktion direkt in Pole und Nullstellen in der z-Ebene um. Die Transformation wird im Folgenden beschrieben, wobei \(T\) die Abtastrate ist.
\(\displaystyle
\frac{\prod\limits_{k=1}^q(s+b_k)}{\prod\limits_{k=1}^p(s+a_k)}
\quad\longrightarrow\quad
\frac{\prod\limits_{k=1}^q(1-e^{-b_kT}z^{-1})}{\prod\limits_{k=1}^p(1-e^{-a_kT}z^{-1})}
\label{matchedz_def}
\)
Die Analyse der Transformationsgleichung zeigt, dass die transformierten Pole der z-Ebene identisch mit den Polen sind, die mit der impulsinvarianten Methode erhalten wurden. Es ist jedoch zu beachten, dass die Positionen der Nullstellen unterschiedlich sind, da die impulsinvariante Methode sie nicht transformieren kann.
Für diese Methode steht der ASN-Filterscript-Befehl \(\texttt{mztrans}\) zur Verfügung.
Ein ausführliches Beispiel
Um die Einfachheit der Transformation von analogen Filtern in ihre diskreten/digitalen Äquivalente mit Hilfe der Analog-Diskret-Transformation zu demonstrieren, folgt nun ein Beispiel für die Modellierung mit der BZT für ein analoges Tiefpassfilter 2ter Ordnung.
Ein verallgemeinertes analoges Tiefpassfilter 2. Ordnung ist gegeben durch:
\(\displaystyle
H(s)=\frac{w_c^2}{s^2+2\zeta w_c s + w_c^2}
\)
wobei \(w_c=2\pi f_c\) die Grenzfrequenz ist und \(\zeta\) die Dämpfung des Filters bestimmt, wobei ein \(\zeta=1/\sqrt{2}\) als kritisch gedämpft oder gleich -3dB bei \(w_c\) gillt. Viele Analog-Ingenieure entscheiden sich dafür, einen Qualitätsfaktor, \(Q = \displaystyle\frac{1}{2\zeta}\) oder Peaking-Faktor für ihre Designs zu spezifizieren. Setzt man \(Q\) in \(H(s)\)ein, erhält man:
\(\displaystyle
H(s)=\frac{w_c^2}{s^2+ \displaystyle{\frac{w_c}{Q}s} + w_c^2}
\)
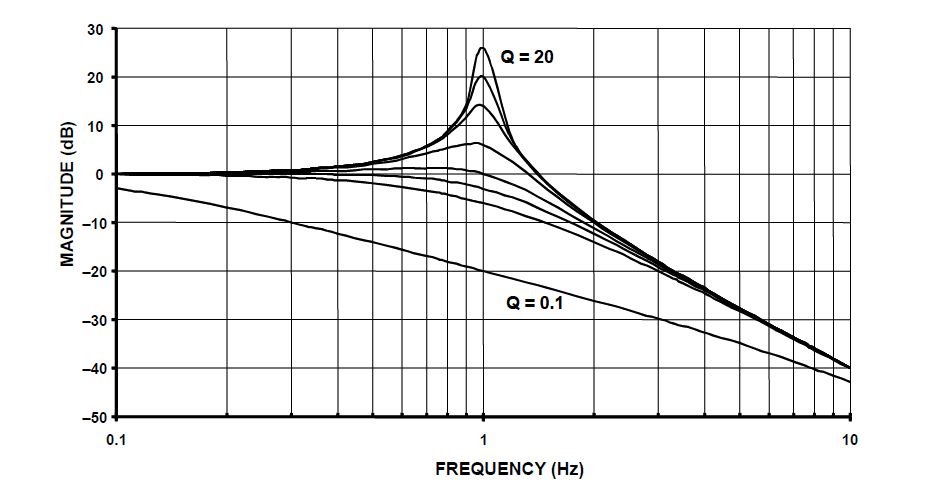
Bei der Analyse von \(H(s)\) fällt auf, dass \(Q=1/\sqrt{2} = 0.707\) ebenfalls zu einer kritisch gedämpften Reaktion führt. Verschiedene Werte von \(Q\) sind unten gezeigt und wie zu sehen ist, treten bei \(Q>1/\sqrt{2}\) peaking auf.
Prototypisches Magnituden Spektrum eines Tiefpassfilters 2. Ordnung für verschiedene Werte von Q:
Beachten Sie, dass bei \(Q>1/\sqrt{2}\) Peaking auftritt.
Bevor die BZT in ASN FilterScript angewendet wird, muss die analoge Übertragungsfunktion in einem analogen Filterobjekt angegeben werden. Der folgende Code richtet ein analoges Filterobjekt für den hier betrachteten Tiefpassprototyp 2:
Main()
wc=2*pi*fc;
Nb={0,0,wc^2};
Na={1,wc/Q,wc^2};
Ha=analogtf(Nb,Na,1,"symbolic"); // make analog filter object
Das Schlüsselwort \(\texttt{symbolic}\) kerzeugt eine symbolische Darstellung der Übertragungsfunktion im Befehlsfenster. Für eine Abtastrate von \(f_s=500Hz\) und \(f_c=30Hz\) und \(Q=0.707\), erhalten wir:
Anwendung der BZT mit den \(\texttt{bilinear}\) Befehl ohne Prewarping,
Hd=bilinear(Ha,0,"symbolic");
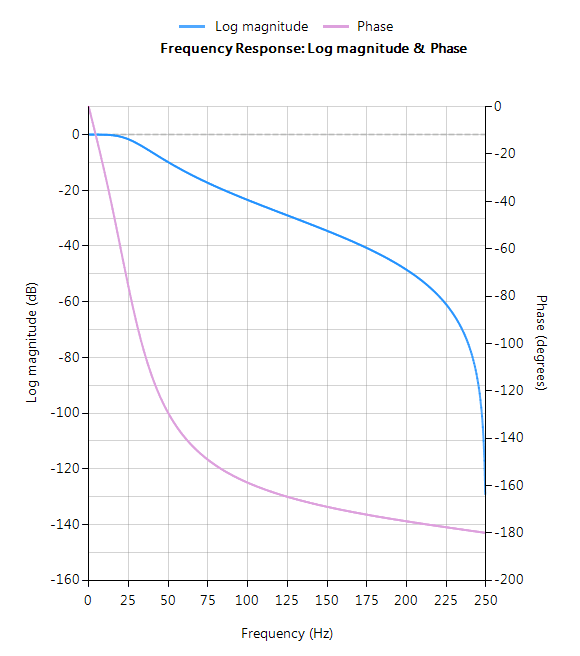
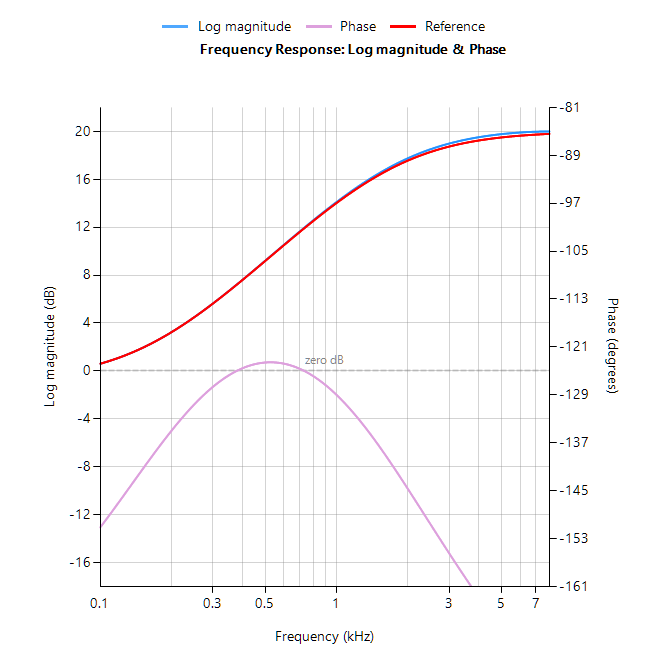
Der vollständige Frequenzgang des transformierten digitalen Filters ist unten gezeigt, wobei zu sehen ist, dass bei \(30Hz\) der Betrag \(-3dB\) und die Phase \( -90^{\circ}\) beträgt, was wie erwartet ist. Beachten Sie auch, wie der Amplituden-Roll-Off des Filters durch das doppelte Nullpaar bei Nyquist beeinflusst wird (siehe das Diagramm der z-Ebene unten), was zu Unterschieden zu seinem analogen Cousin führt. 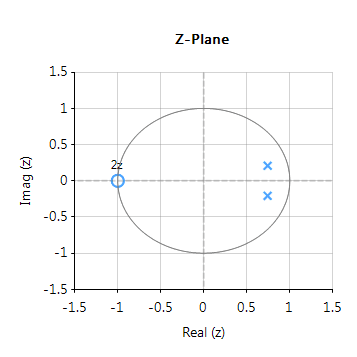
Die Pol-Null-Positionen können in ASN Filterscript oder über den interaktiven Pol-Null-Z-Ebenen-Plot-Editor des ASN Filter Designers mit der Maus verändert werden!
Implementierung
Der vollständige Code zum Umwandeln eines verallgemeinerten analogen Tiefpassfilter-Prototyps 2. Ordnung in sein digitales Äquivalent unter Verwendung der BZT über ASN FilterScriptist unten angegeben:
ClearH1; // clear primary filter from cascade
interface Q = {0.1,10,0.02,0.707};
interface fc = {10,200,10,40};
Main()
wc=2*pi*fc;
Nb={0,0,wc^2};
Na={1,wc/Q,wc^2};
Ha=analogtf(Nb,Na,1,"symbolic"); // make analog filter object
Hd=bilinear(Ha,0,"symbolic"); // transform Ha via BZT into digital object, Hd
Num=getnum(Hd);
Den=getden(Hd);
Gain=getgain(Hd);