All-pass filters
All-pass filters bieden een eenvoudige manier om de faserespons van een IIR te wijzigen of te verbeteren zonder de omvang ervan te beïnvloeden. Als zodanig worden ze meestal aangeduid als fase-equalizers en hebben ze een bijzondere toepassing gevonden in digitale audiotoepassingen.
In zijn eenvoudigste vorm kan een filter worden opgebouwd uit een eerste orde transfer functie:
\( A(z)=\Large{\frac{r+z^{-1}}{1+r z^{-1}}} \, \, \normalsize{; r<1} \)
Merk bij \(\small A(z)\) op, dat de pool en de nul op de echte z-vlakas liggen en dat de pool bij de radius \(\small r\) een nul bij radius \(\small 1/r\) heeft. Zodanig dat de polen en nullen wederkerig zijn met elkaar. Deze eigenschap is de sleutel tot het all-pass filterconcept. Zoals we nu zullen zien door het concept verder uit te breiden naar een tweede orde all-pass filter:
\( A(z)=\Large\frac{r^2-2rcos \left( \frac{2\pi f_c}{fs}\right) z^{-1}+z^{-2}}{1-2rcos \left( \frac{2\pi f_c}{fs}\right)z^{-1}+r^2 z^{-2}} \)
Waarbij \(\small f_c\) de middenfrequentie is, \(\small r\) de radius of van de polen is en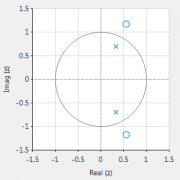 
\(\small f_s\) de sampling frequency. Merk op dat de teller en noemer coefficienten zijn weergegeven als
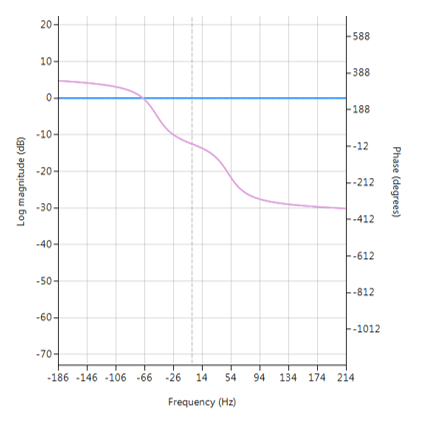Frequentierespons van het all-pass filter:
Let op de constante omvang van het spectrum (weergegeven in blauw).
Implementatie
Een All-pass filter kan geimplementeerd worden in ASN FilterScript als volgt:
[code language=”java”]
ClearH1; // clear primary filter from cascade
interface radius = {0,2,0.01,0.5}; // radius value
interface fc = {0,fs/2,1,fs/10}; // frequency value
Main()
Num = {radius^2,-2*radius*cos(Twopi*fc/fs),1};
Den = reverse(Num); // mirror image of Num
Gain = 1;
[/code]
Voor een gedetailleerde beschrijving van de IIR-faseregelaar en de APF (all-pass filter) ontwerptool van de ASN-filterontwerper, zie het volgende artikel.
