Bien que la conception de filtres RIF à phase linéaire soit une tâche facile, ce n’est certainement pas le cas pour les filtres RII qui ont généralement une réponse en phase hautement non linéaire, en particulier autour des fréquences de coupure du filtre. Cet article traite des caractéristiques nécessaires pour qu’un filtre numérique ait une phase linéaire, et de la façon dont la phase de la bande passante d’un filtre RII peut être modifiée afin d’obtenir une phase linéaire en utilisant des filtres d’égalisation passe-tout.
Pourquoi avons-nous besoin de filtres à phase linéaire ?
Les filtres numériques à phase linéaire ont l’avantage de retarder toutes les composantes de fréquence de la même quantité, c’est-à-dire qu’ils préservent les relations de phase du signal d’entrée. Cette préservation de la phase signifie que le signal filtré conserve la forme du signal d’entrée original. Cette caractéristique est essentielle pour les applications audio, car la forme du signal est primordiale pour maintenir une haute fidélité dans le son filtré. L’analyse biomédicale des formes d’onde ECG est un autre domaine d’application qui requiert cette caractéristique, car tout artefact introduit par le filtre peut être interprété à tort comme une anomalie cardiaque.
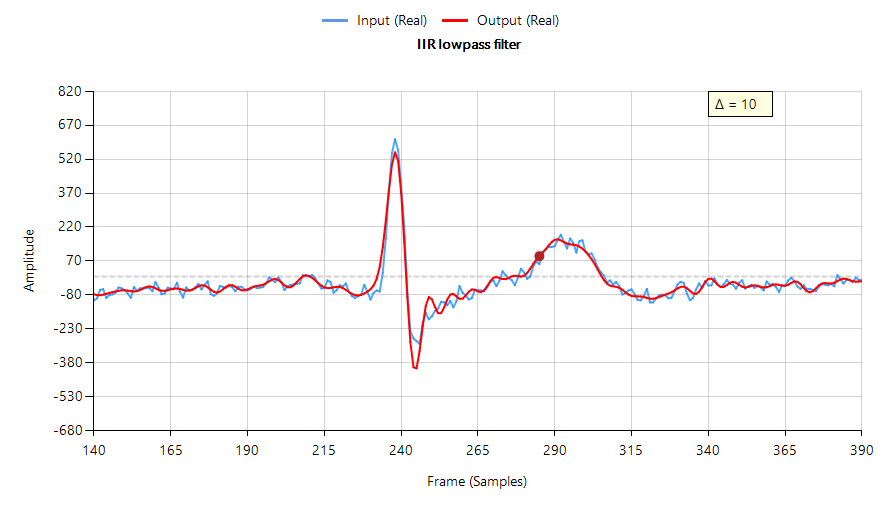
Le graphique suivant montre les performances de filtrage d’un filtre passe-bas RII de type I de Chebyshev sur des données ECG – la forme d’onde d’entrée (représentée en bleu) est décalée de 10 échantillons (\(\small \Delta=10\)) pour compenser approximativement le retard de groupe du filtre. Remarquez que le signal filtré (représenté en rouge) a atténué, élargi et ajouté des oscillations autour du pic ECG, ce qui n’est pas souhaitable.
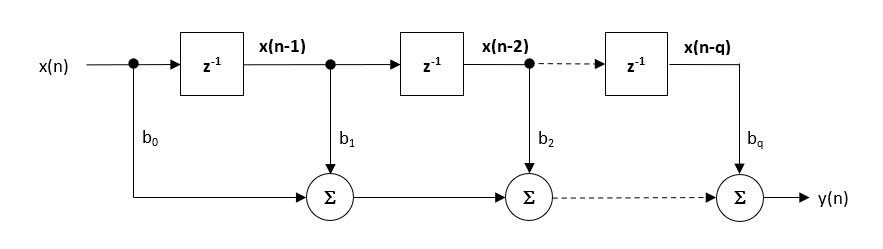
Pour qu’un filtre numérique ait une phase linéaire, sa réponse impulsionnelle doit présenter une symétrie conjuguée-paire ou conjuguée-impaire autour de son point central. Ceci est facilement visible pour un filtre RIF,
Avec la contrainte suivante sur ses coefficients ,
ce qui conduit à ,
En analysant l’équation 3, nous voyons que les racines (zéros) de \(\small H(z)\) doivent aussi être les zéros de \(\small H^\ast (1/z^\ast)\). Cela signifie que les racines de H(z) doivent apparaître par paires réciproques conjuguées, c’est-à-dire que si \(\small z_k\) est un zéro de \(\small H(z)\), alors \(\small H^\ast (1/z^\ast)\) doit aussi être un zéro.
Pourquoi les filtres RII n’ont pas une phase linéaire
Un filtre numérique est dit stable à Entrée Bornée, Sortie Bornée, ou stable EBSB (stable BIBO), si chaque entrée bornée donne lieu à une sortie bornée. Tous les filtres RII ont soit des pôles, soit à la fois des pôles et des zéros, et doivent être stables EBSB, c’est-à-dire que
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty \tag{4}\)
Où, \(\small h(k)\) est la réponse impulsionnelle du filtre. En analysant l’équation 4, il devrait être clair que le critère de stabilité EBSB ne sera satisfait que si les pôles du système se trouvent à l’intérieur du cercle unitaire, puisque la ROC (région de convergence) du système doit inclure le cercle unitaire. Par conséquent, il suffit de dire qu’un signal d’entrée borné produira toujours un signal de sortie borné si tous les pôles se trouvent à l’intérieur du cercle unitaire.
Les zéros, par contre, ne sont pas contraints par cette exigence et, par conséquent, peuvent se trouver n’importe où sur le plan z, puisqu’ils n’affectent pas directement la stabilité du système. Par conséquent, une analyse de la stabilité du système peut être entreprise en calculant d’abord les racines de la fonction de transfert (c’est-à-dire les racines des polynômes du numérateur et du dénominateur), puis en traçant les pôles et les zéros correspondants sur le plan z.
En appliquant la logique développée aux pôles d’un filtre RII, nous arrivons maintenant à une conclusion très importante sur la raison pour laquelle les filtres RII ne peuvent pas avoir une phase linéaire.
Un filtre stable EBSB doit avoir ses pôles à l’intérieur du cercle unitaire. Pour obtenir une phase linéaire, un filtre RII devrait avoir des pôles réciproques conjugués à l’extérieur du cercle unitaire, ce qui le rendrait instable EBSB.
Sur la base de cette affirmation, il semblerait qu’il ne soit pas possible de concevoir un RII pour avoir une phase linéaire. Cependant, comme nous le verrons plus loin, des filtres d’égalisation de phase peuvent être utilisés pour linéariser la réponse en phase de la bande passante.
Linéarisation de phase avec des filtres passe-tout
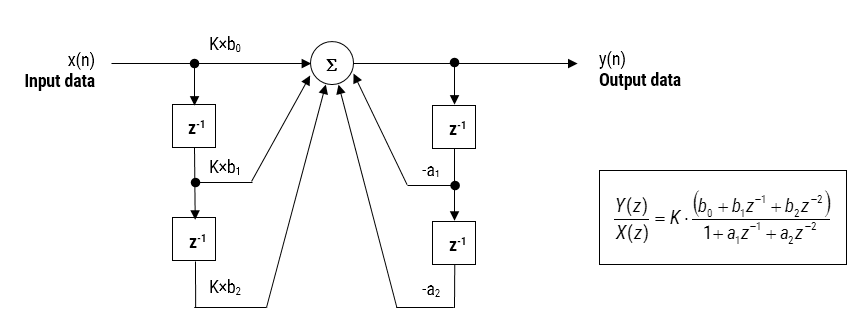
Les filtres passe-tout (equalisers) de linéarisation de phase (égaliseurs) sont une méthode bien établie pour modifier la réponse en phase d’un filtre sans affecter sa réponse en amplitude. Un filtre passe-tout du second ordre (Biquad) est défini comme suit :
Où \(\small f_c\) est la fréquence centrale, \(\small r\) est le rayon des pôles et \(\small f_s\) est la fréquence d’échantillonnage. Remarquez comment les coefficients du numérateur et du dénominateur sont disposés comme une paire d’images miroir l’une de l’autre. La propriété d’image miroir est ce qui donne au filtre passe-tout sa propriété souhaitable, à savoir permettre au concepteur de modifier la réponse en phase tout en gardant la réponse en magnitude constante ou plate sur l’ensemble du spectre de fréquences.
En cascadant une cascade d’égalisation APF (filtre passe-tout) (composée de plusieurs APF) avec un filtre RII, l’idée de base est que nous n’avons besoin de linéariser la réponse en phase que dans la région de la bande passante. Les autres régions, telles que la bande de transition et la bande d’arrêt, peuvent être ignorées, car toute non-linéarité dans ces régions est de peu d’intérêt pour le résultat global du filtrage.
Le défi
La cascade d’APF semble être un compromis idéal pour ce défi, mais en réalité, il faut beaucoup de temps et un réglage très précis des positions des APF pour obtenir un résultat acceptable. Chaque APF a deux variables : \(\small f_c\) et \(\small r\) qui doivent être optimisées, ce qui complique la solution. Celle-ci est encore compliquée par le fait que plus on ajoute d’étages d’APF à la cascade, plus le délai de groupe (latence) du filtre global devient élevé. Ce dernier point peut devenir problématique pour les systèmes de contrôle en boucle fermée en temps réel qui dépendent de la propriété de faible latence d’un RII.
Néanmoins, malgré ces difficultés, l’égaliseur APF est un bon compromis pour linéariser les caractéristiques de phase de la bande passante d’un RII.
L’égaliseur APF
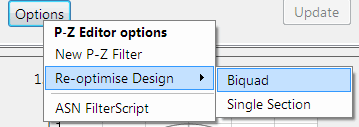
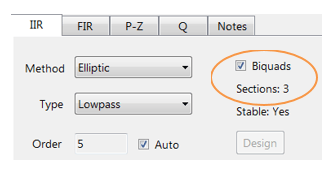
ASN Filter Designer fournit aux concepteurs une interface graphique d’égaliseur tout-phase très simple à utiliser pour linéariser la phase de bande passante des filtres RII. Comme on peut le voir ci-dessous, l’interface est très intuitive, et permet aux concepteurs de placer rapidement et d’affiner les positions des filtres APF avec la souris. L’outil calcule automatiquement \(\small f_c\) et \(\small r\), en fonction de la position du marqueur.
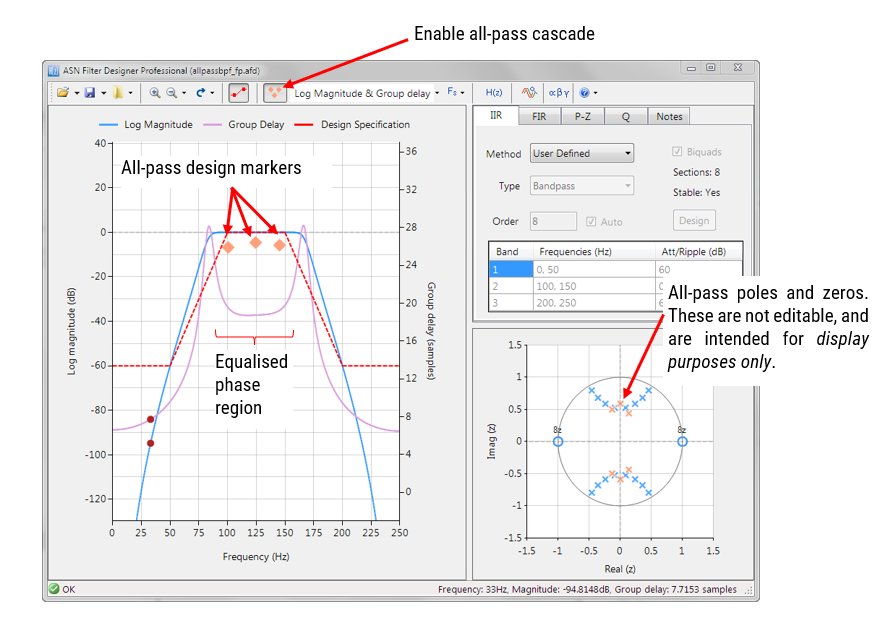
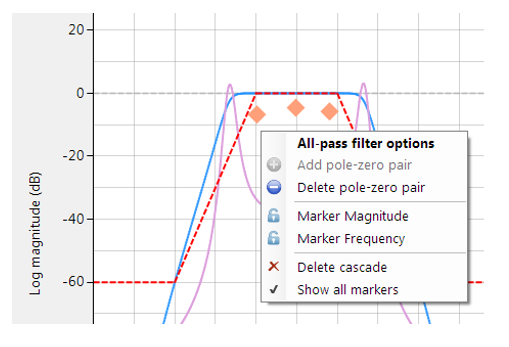
Un clic droit sur le diagramme de réponse en fréquence ou sur un marqueur de conception passe-tout existant affiche un menu d’options, comme illustré à gauche.
Vous pouvez ajouter jusqu’à 10 biquads (version professionnelle uniquement).
Un RII avec une phase de bande passante linéaire
En concevant un égaliseur composé de trois paires d’APF, et en le cascadant avec le filtre de Chebyshev de la figure 1, nous obtenons une forme d’onde de filtre dont le pic est beaucoup plus net, avec moins d’atténuation et d’oscillation que le RII original – voir ci-dessous. Toutefois, cette amélioration se fait au prix de trois filtres Biquad supplémentaires (la cascade APF) et d’un retard de groupe accru, qui passe à 24 échantillons contre 10 à l’origine.
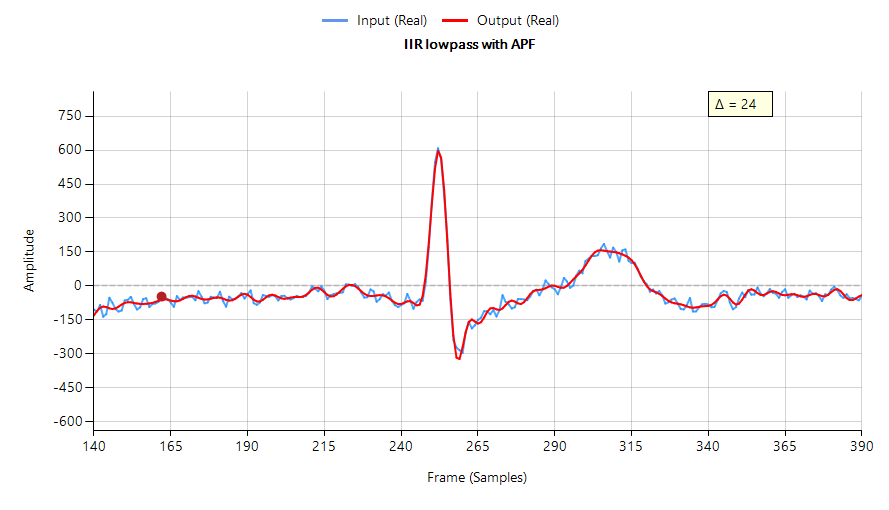
(distorsion de phase minimale)
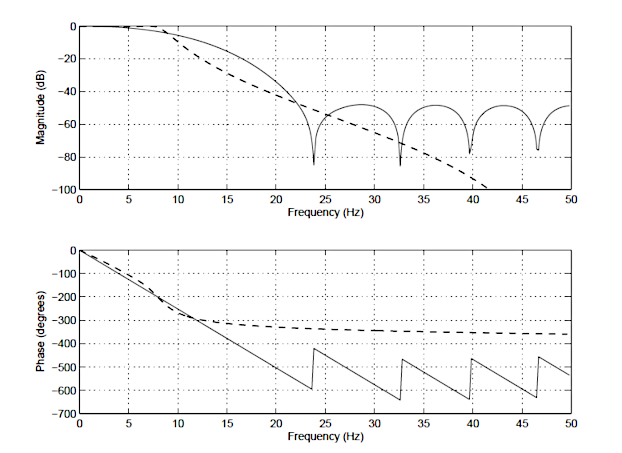
La réponse en fréquence du filtre RII original et du filtre RII égalisé est illustrée ci-dessous, où le retard de groupe (en violet) est le retard moyen du filtre et constitue un moyen plus simple d’évaluer la linéarité.
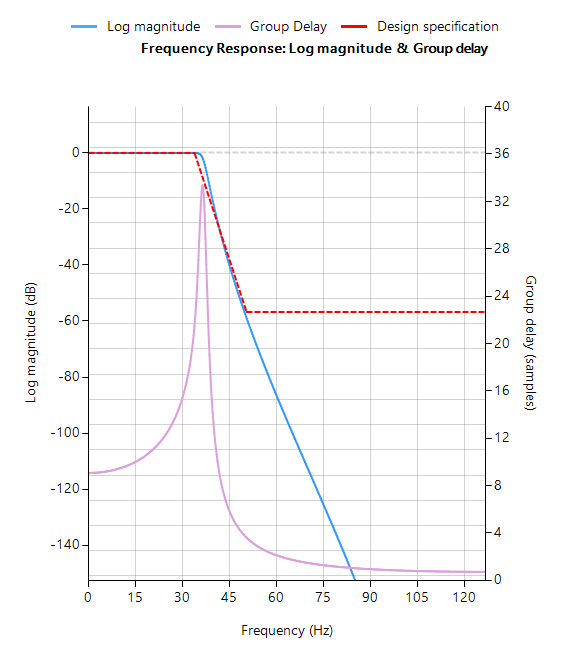
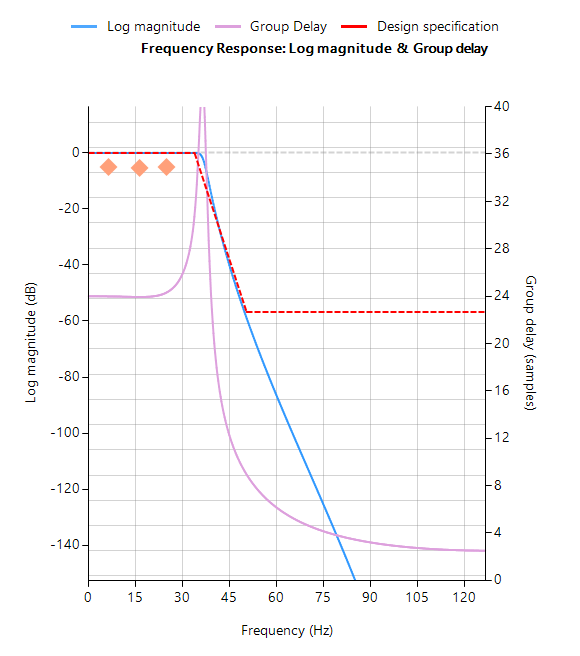
Remarquez que le temps de propagation de groupe de la bande passante RII égalisée (illustré à droite) est presque plat, ce qui confirme que la phase est effectivement linéaire.
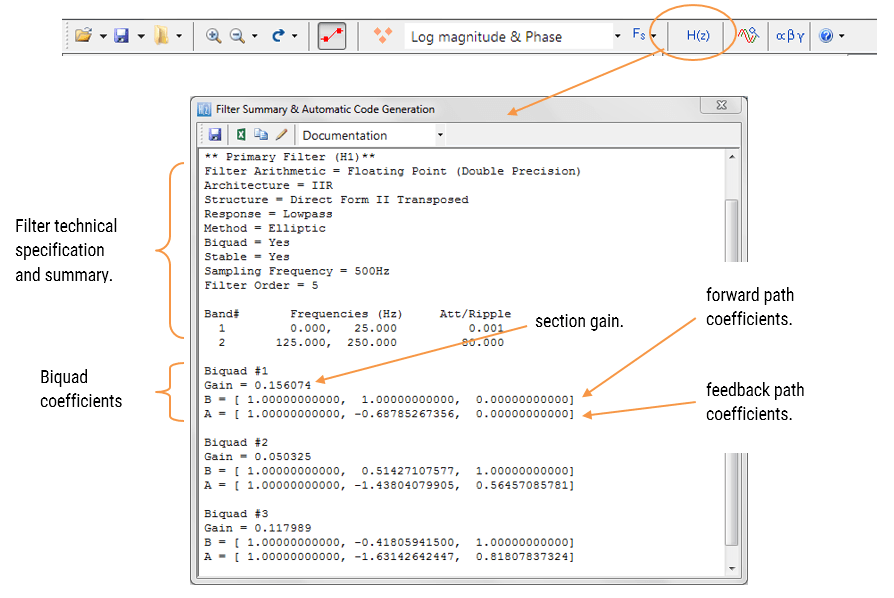
Génération automatique de code vers les cœurs de processeurs Arm via CMSIS-DSP
Le moteur de génération automatique de code de l’ASN Filter Designer facilite l’exportation d’un filtre conçu vers des processeurs basés sur Cortex-M Arm via le cadre logiciel CMSIS-DSP. Les fonctions d’analyse et d’aide intégrées de l’outil aident le concepteur à configurer avec succès la conception pour le déploiement.
Avant de générer le code, les filtres RII et d’égalisation (c’est-à-dire les filtres H1 et Heq) doivent d’abord être réoptimisés (fusionnés) en une structure de filtre H1 (filtre principal) pour le déploiement. Le menu d’options se trouve sous l’onglet P-Z dans l’interface utilisateur principale.
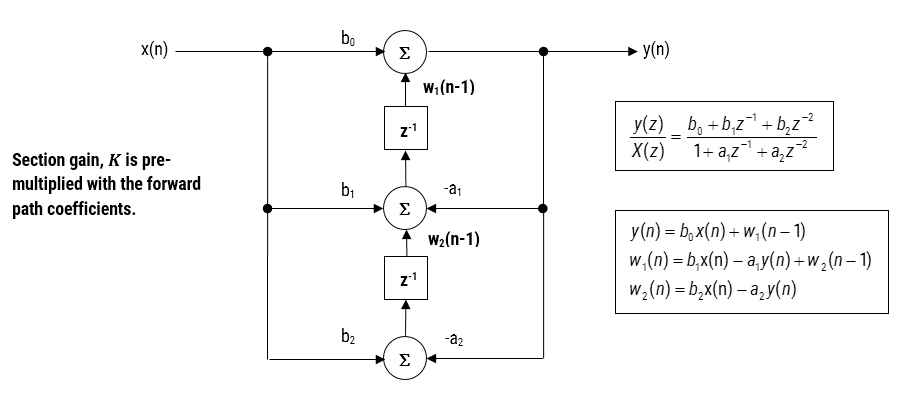
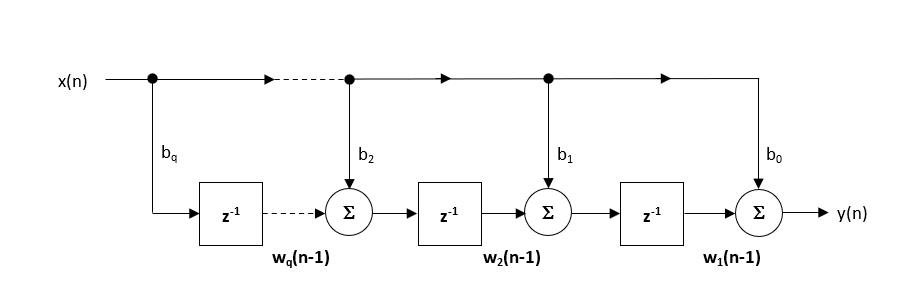
Toutes les conceptions de filtres RII en virgule flottante doivent être basées sur l’arithmétique en simple précision et sur une structure de filtre de Direct Form I ou Direct Form II Transposed, car celle-ci est prise en charge par un multiplicateur matériel dans les cœurs M4F, M7F, M33F et M55F. Bien que vous puissiez choisir la double précision, la prise en charge matérielle n’est disponible que dans certains dispositifs Hélium M7F et M55F. La structure Direct Form II Transposed est préconisée pour l’implémentation en virgule flottante en raison de sa plus grande précision numérique.
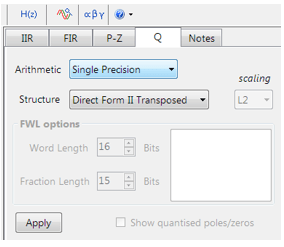
Les paramètres de quantification et de structure de filtre se trouvent sous l’onglet Q (comme illustré à gauche). En réglant l’Arithmetic sur Single Precision et la Structure sur strong>Direct Form II Transposed et en cliquant sur le bouton Apply, on configure le RII considéré ici pour le cadre logiciel CMSIS-DSP.
Sélectionnez le cadre Arm CMSIS-DSP dans la boîte de sélection de la fenêtre de résumé du filtre:
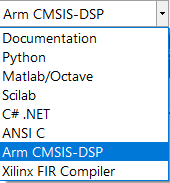
Le code C généré automatiquement basé sur le cadre CMSIS-DSP pour une implémentation directe sur un processeur Cortex-M basé sur Arm est montré ci-dessous :
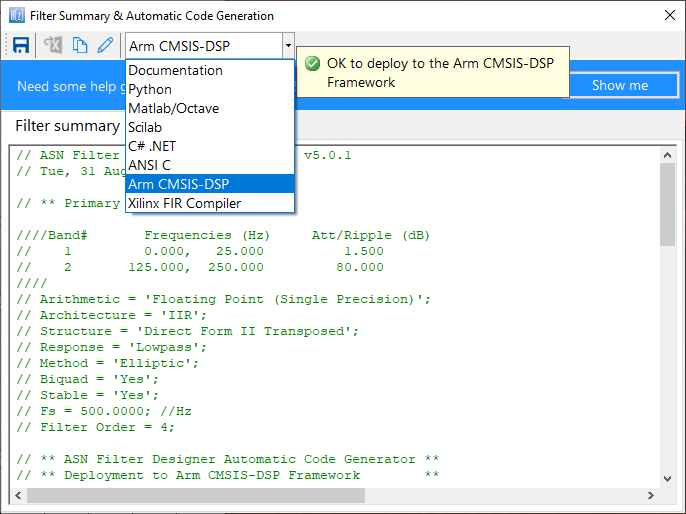
Le générateur de code automatique de l’ASN Filter Designer génère tout le code d’initialisation, la mise à l’échelle et les structures de données nécessaires pour implémenter le filtre RII linéarisé via la bibliothèque CMSIS-DSP d’Arm.
Assistant de déploiement Arm
Les utilisateurs de la licence professionnelle peuvent accélérer le déploiement en utilisant l’assistant de déploiement Arm. L’IA intégrée déterminera automatiquement les meilleurs paramètres pour votre conception en fonction des paramètres de quantification choisis.
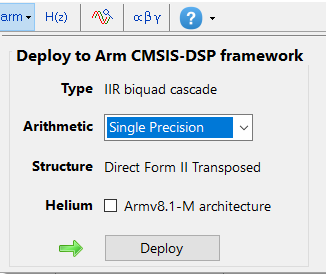
L’IA intégrée analyse automatiquement votre cascade de filtres complète et convertit tous les filtres H2 ou Heq en H1 pour la mise en œuvre.
Qu’avons-nous appris ?
Les racines d’un filtre numérique à phase linéaire doivent se trouver dans des paires réciproques conjuguées. Bien que cela ne pose aucun problème pour un filtre RIF, cela devient infaisable pour un filtre RII, car les pôles devraient se trouver à la fois à l’intérieur et à l’extérieur du cercle unitaire, ce qui rendrait le filtre instable EBSB.
La réponse en phase de la bande passante d’un filtre RII peut être linéarisée en utilisant une cascade d’égalisation APF. Le Filter Designer d’ASN fournit aux concepteurs tout ce dont ils ont besoin via une interface graphique d’égaliseur de phase passe-tout très simple à utiliser, afin de concevoir une cascade APF appropriée en utilisant simplement la souris !
Le filtre RII linéarisé peut être exporté via le générateur de code automatique utilisant les fonctions optimisées de la bibliothèque CMSIS-DSP d’Arm pour être déployé sur n’importe quel microcontrôleur Cortex-M.