Der Unterschied zwischen IIR- und FIR-Filtern: ein praktischer Leitfaden
Ein digitaler Filter ist ein mathematischer Algorithmus, der mit einem digitalen Datensatz (z.B. Sensordaten) arbeitet, um Informationen von Interesse zu extrahieren und unerwünschte Informationen zu entfernen. Zu den Anwendungen dieser Art von Technologie gehören die Entfernung von Störimpulsen aus Sensordaten oder sogar die Bereinigung von Rauschen auf einem gemessenen Signal zur leichteren Datenanalyse. Aber wie wählen wir den besten Typ von Digitalfilter für unsere Anwendung aus? Und was sind die Unterschiede zwischen einem IIR-Filter und einem FIR-Filter?
Digitale Filter werden in die folgenden zwei Kategorien unterteilt:
- Unendliche Impulsantwort (Infinite impulse response , IIR)
- Endliche Impulsantwort (Finite impulse response, FIR)
Wie die Namen vermuten lassen, wird jeder Filtertyp nach der Länge seiner Impulsantwort kategorisiert. Bevor man jedoch mit einer detaillierten mathematischen Analyse beginnt, ist es ratsam, die Unterschiede in der Leistung und den Eigenschaften der einzelnen Filtertypen zu berücksichtigen.
Beispiel
Um die Unterschiede zwischen einem IIR und einem FIR zu veranschaulichen, ist der Frequenzgang eines FIR 14. Ordnung (durchgezogene Linie) und eines Tschebyscheff Typ I IIR 4. Ordnung (gestrichelte Linie) unten in Abbildung 1 dargestellt. Beachten Sie, dass das Phasenspektrum des IIR-Filters, obwohl die Magnituden Spektren einen ähnlichen Dämpfungsgrad aufweisen, im Durchlassbereich (\(\small 0\rightarrow7.5Hz\)) nichtlinear ist und bei der Grenzfrequenz, \(\small f_c=7.5Hz\) sehr nichtlinear wird. Beachten Sie auch, dass das FIR eine höhere Anzahl von Koeffizienten benötigt (15 gegenüber den 10 des IIR), um die Dämpfungseigenschaften des IIR anzupassen.
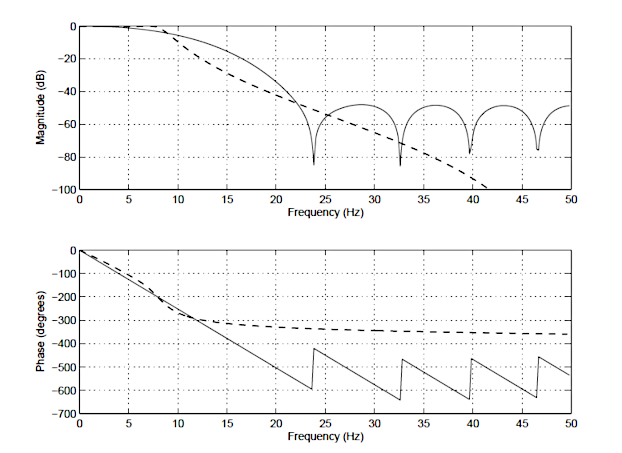
Dies sind nur einige der Unterschiede zwischen den beiden Filtertypen. Eine detaillierte Zusammenfassung der wichtigsten Vor- und Nachteile jedes Filtertyps folgt jetzt.
IIR-filter
IIR-Filter (unendliche Impulsantwort) werden im Allgemeinen für Anwendungen gewählt, bei denen die lineare Phase nicht allzu wichtig ist und der Speicher begrenzt ist. Sie wurden in großem Umfang in der Audioentzerrung, der biomedizinischen Sensorsignalverarbeitung, intelligenten IoT/IIoT-Sensoren und Hochgeschwindigkeits-Telekommunikations-/RF-Anwendungen eingesetzt.
Vorteile
- Niedrige Implementierungskosten: Benötigt weniger Koeffizienten und Speicherplatz als FIR-Filter, um einen ähnlichen Satz von Spezifikationen, d.h. Grenzfrequenz und Sperrdämpfung, zu erfüllen
- Niedrige Latenzzeit: eignet sich aufgrund der geringen Anzahl von Koeffizienten für Echtzeitsteuerung und sehr schnelle HF-Anwendungen
- Analoges Äquivalent: Kann zur Nachahmung der Eigenschaften von analogen Filtern unter Verwendung von s-z-Ebenen-Abbildungstransformationen verwendet werden
Nachteile
- Nicht-lineare Phaseneigenschaften: Die Phaseneigenschaften eines IIR-Filters sind im Allgemeinen nichtlinear, insbesondere in der Nähe der Grenzfrequenzen. Um die Phasencharakteristik im Durchlassbereich zu verbessern, können Allpass-Entzerrungsfilter verwendet werden
- Detailliertere Analyse: Erfordert mehr Skalierung und numerische Überlaufanalyse, wenn sie in Festkommaform implementiert wird. Die direkte Form II-Filterstruktur ist besonders empfindlich gegenüber den Auswirkungen der Quantisierung und erfordert besondere Sorgfalt während der Entwurfsphase
- Numerische Stabilität: Aufgrund der Rückkopplungspfade numerisch weniger stabil als ihre FIR-Pendants (finite impulse Response)
FIR-filter
FIR-Filter (FIR = Finite Impuls Response) werden im Allgemeinen für Anwendungen gewählt, bei denen eine lineare Phase wichtig ist und eine angemessene Menge an Speicher und Rechenleistung zur Verfügung steht. Sie haben eine weite Verbreitung in Audio- und biomedizinischen Signalverbesserungsanwendungen. Ihre Nullstruktur (siehe unten) stellt sicher, dass sie für jede Art von Eingangssignal niemals instabil werden, was ihnen einen deutlichen Vorteil gegenüber dem IIR verleiht.
Vorteile
- Lineare Phase: FIRs können leicht so ausgelegt werden, dass sie eine lineare Phase haben. Dies bedeutet, dass keine Phasenverzerrung in das zu filternde Signal eingebracht wird, da alle Frequenzen um den gleichen Betrag in der Zeit verschoben sind – und somit ihre relativen harmonischen Beziehungen (d.h. konstante Gruppen- und Phasenverzögerung) beibehalten werden. Dies ist bei IIR-Filtern, die eine nichtlineare Phasencharakteristik haben, sicher nicht der Fall
- Stabilität: Da FIRs keine früheren Ausgangswerte zur Berechnung ihres aktuellen Ausgangs verwenden, d.h. sie haben keine Rückkopplung, können sie für jede Art von Eingangssignal niemals instabil werden, was ihnen einen deutlichen Vorteil gegenüber IIR-Filtern verschafft.
- Arbiträrer Frequenzgang: Die Funktion firarb() von Parks-McClellan und ASN FilterScript ermöglicht den Entwurf einer FIR mit einem beliebigen Betragsverlauf. Dies bedeutet, dass eine FIR leichter angepasst werden kann als ein IIR
Fixpunktleistung: Die Auswirkungen der Quantisierung sind weniger schwerwiegend als die eines IIR
Nachteile
- Hoher Rechen- und Speicherbedarf: FIRs benötigen in der Regel viel mehr Koeffizienten für das Erreichen einer scharfen Hell-Dunkel-Grenze als ihre IIR-Pendants. Dies hat zur Folge, dass sie viel mehr Speicher und eine deutlich höhere Anzahl von MAC-Operationen (multiple and accumulate) benötigen. Moderne Mikrocontroller-Architekturen, die auf den Cortex-M-Cores des Arm’s basieren, enthalten jetzt jedoch DSP-Hardware-Unterstützung über SIMD (Signalbefehle, multiple Daten), die die Filteroperationen erheblich beschleunigen
- Höhere Latenz: Die höhere Anzahl von Koeffizienten bedeutet, dass ein FIR im Allgemeinen für schnelle Anwendungen mit hohem Durchsatz weniger geeignet ist als ein IIR. Problematisch wird dies bei Echtzeit-Regelanwendungen, bei denen ein FIR-Filter möglicherweise eine zu große Gruppenverzögerung aufweist, um die Stabilität der Schleife zu erreichen
- Kein analoges Äquivalent: Mit Hilfe der Bilinearen, angepassten z-Transformation(s-z-Mapping) kann ein analoges Filter leicht in ein äquivalentes IIR-Filter umgewandelt werden. Bei einem FIR-Filter ist dies jedoch nicht möglich, da es kein analoges Äquivalent gibt
Mathematische Definitionen
Wie in der Einleitung besprochen, stammen die Namen IIR und FIR aus den mathematischen Definitionen der einzelnen Filtertypen, d.h. ein IIR-Filter wird nach seiner theoretisch unendlichen Impulsantwort kategorisiert,
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)
und eine FIR, die nach ihrer endlichen Impulsantwort kategorisiert wird,
y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)
\)
Wir werden nun der Reihe nach den mathematischen Eigenschaften der einzelnen Filtertypen analysieren.
IIR-Definition
Wie oben gesehen, wird ein IIR-Filter nach seiner theoretisch unendlichen Impulsantwort kategorisiert,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x(n-k) \)
Praktisch gesehen ist es nicht möglich, den Ausgang einer IIR mit dieser Gleichung zu berechnen. Daher kann die Gleichung in Form einer endlichen Anzahl von Polen \(small p\) und Nullen \(small q\) umgeschrieben werden, wie durch die lineare Konstante Koeffizienten-Differenzgleichung definiert, die durchgegeben ist:
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
wobei \(small a_k\) und \(small b_k\) die Nenner- und Zähler-Polynomkoeffizienten des Filters sind, deren Wurzeln gleich den Polen bzw. Nullen des Filters sind. Daher kann eine Beziehung zwischen der Differenzengleichung und der z-Transformation (Übertragungsfunktion) definiert werden, indem die Verzögerungseigenschaft der z-Transformation so verwendet wird, dass
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
\)
Wie man sieht, ist die Übertragungsfunktion eine Frequenzbereichsdarstellung des Filters. Beachten Sie auch, dass die Pole auf die Ausgangsdaten und die Nullen auf die Eingangsdaten wirken. Da die Pole auf die Ausgangsdaten einwirken und die Stabilität beeinflussen, ist es für die BIBO-Stabilität (BIBO = bounded input, bounded output) wichtig, dass ihre Radien innerhalb des Einheitskreises bleiben (d.h. <1). Die Radien der Nullen sind weniger kritisch, da sie die Filterstabilität nicht beeinflussen. Dies ist der Hauptgrund, warum FIR-Filter (FIR = Finite Impulse Response) mit nur Nullen immer stabil sind.
BIBO-Stabilität
Ein lineares zeitinvariantes (LTI) System (wie z.B. ein digitaler Filter) gilt als begrenzter Eingang, begrenzter stabiler Ausgang oder BIBO-stabil, wenn jeder begrenzte Eingang zu einem begrenzten Ausgang führt, wie z.B.
\(\displaystyle \sum_{k=0}^{\infty}\left|h(k)\right|<\infty [/latex] Wo, [latex]\small h(k)[/latex] ist die Impulsantwort des LTI-Systems. Bei der Analyse dieser Gleichung sollte klar sein, dass das BIBO-Stabilitätskriterium nur dann erfüllt ist, wenn die Pole des Systems innerhalb des Einheitskreises liegen, da die ROC (Region of Convergence) des Systems den Einheitskreis einschließen muss. Folglich ist es ausreichend zu sagen, dass ein begrenztes Eingangssignal immer ein begrenztes Ausgangssignal erzeugt, wenn alle Pole innerhalb des Einheitskreises liegen.
Die Nullen hingegen werden durch diese Anforderung nicht eingeschränkt und können folglich überall auf der z-Ebene liegen, da sie die Systemstabilität nicht direkt beeinflussen. Daher kann eine Systemstabilitätsanalyse durchgeführt werden, indem zunächst die Wurzeln der Übertragungsfunktion berechnet werden (d.h. die Wurzeln der Zähler- und Nenner Polynome) und dann die entsprechenden Pole und Nullen auf der z-Ebene aufgetragen werden.
Eine interessante Situation ergibt sich, wenn irgendwelche Pole auf dem Einheitskreis liegen, da das System als geringfügig stabil gilt, da es weder stabil noch instabil ist. Obwohl geringfügig stabile Systeme nicht BIBO-stabil sind, wurden sie von den Entwicklern digitaler Oszillatoren ausgenutzt, da ihre Impulsantwort eine einfache Methode zur Erzeugung von Sinuswellen bietet, die sich im Bereich der Telekommunikation als unschätzbar wertvoll erwiesen haben.
Biquad-IIR-Filter
Die hier besprochene IIR-Filterimplementierung wird als biquad bezeichnet, da sie zwei Pole und zwei Nullen hat, wie in Abbildung 2 unten dargestellt. Die Biquad-Implementierung ist besonders nützlich für Festpunkt-Implementierungen, da die Auswirkungen der Quantisierung und der numerischen Stabilität minimiert werden. Der Gesamterfolg einer Biquad-Implementierung hängt jedoch von der verfügbaren Zahlengenauigkeit ab, die ausreichend sein muss, um sicherzustellen, dass die quantisierten Pole immer innerhalb des Einheitskreises liegen.
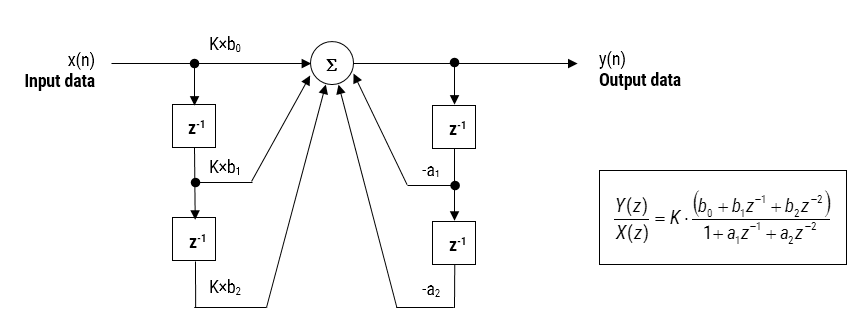
Abbildung 2: Realisierung und Übertragungsfunktion des Direct Form I (Biquad) IIR-Filters
Bei der Analyse von Abbildung 2 wird deutlich, dass die Biquad-Struktur tatsächlich aus zwei Rückkopplungspfaden (skaliert mit a1 und a2), drei Vorkopplungspfaden (skaliert mit b0,b1 und b2) und einer Abschnittsverstärkung [latex]small K\) besteht. Die Filteroperation von Abbildung 1 kann daher durch die folgende einfache rekursive Gleichung zusammengefasst werden:
\(\displaystyle y(n)=K\times\Big[b_0 x(n) + b_1 x(n-1) + b_2 x(n-2)\Big] – a_1 y(n-1)-a_2 y(n-2)\)
Bei der Analyse der Gleichung ist zu beachten, dass die Biquad-Implementierung nur vier Additionen (mit nur einem Akkumulator) und fünf Multiplikationen erfordert, die leicht auf jedem Cortex-M-Mikrocontroller untergebracht werden können. Die Querschnittsverstärkung \(small K\) kann vor der Implementierung auch mit den Vorwärtspfad-Koeffizienten vormultipliziert werden.
Eine Sammlung von Biquad-Filtern wird als Biquad-Kaskade bezeichnet, wie unten dargestellt.

Der ASN Filter Designer kann eine Kaskade von bis zu 50 Biquads entwerfen und implementieren (nur Professional Edition).
Fließkomma-Implementierung
Bei der Implementierung eines Fließkommafilters (d.h. bei Verwendung von Arithmetik mit doppelter oder einfacher Genauigkeit) gelten direkte Form II-Strukturen als bessere Wahl als die direkte Form I-Struktur. Die Direkte Form II Transponierte Struktur gilt als die numerisch genaueste für die Implementierung in Fließkomma-Arithmetik, da die unerwünschten Effekte der numerischen Überfüllung durch die Analyse der Differenzgleichungen minimiert werden
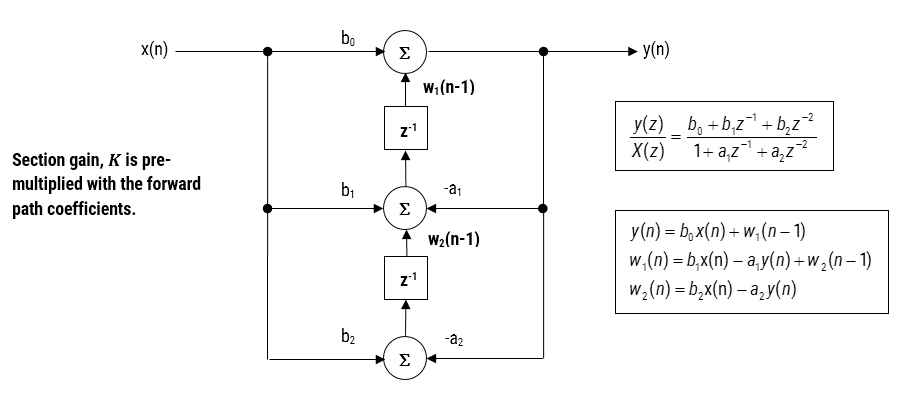
Abbildung 3 – Direkte Form II Transponierte Struktur-, Übertragungsfunktions- und Differenzgleichungen
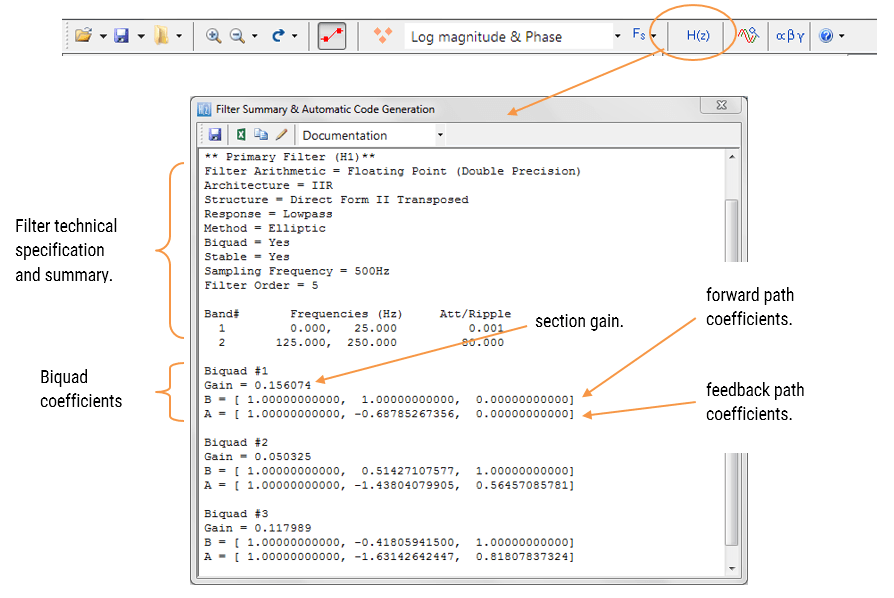
Die Filterzusammenfassung (in Abbildung 4 dargestellt) bietet dem Konstrukteur einen detaillierten Überblick über den entworfenen Filter, einschließlich einer detaillierten Zusammenfassung der technischen Spezifikationen und der Filterkoeffizienten, was einen schnellen und einfachen Weg zur Dokumentation Ihres Entwurfs darstellt.
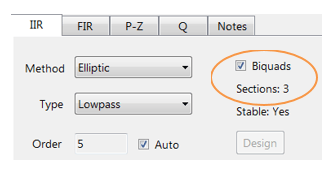
Der ASN-Filter-Designer unterstützt den Entwurf und die Implementierung sowohl von Einzelabschnitt- als auch von Biquad- (Standardeinstellung) IIR-Filtern.
FIR-Definition
Rückgabe der linearen Konstanten-Koeffizienten-Differenzgleichung des IIR, d.h.
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
Beachten Sie, dass, wenn wir die \(small a_k\) Koeffizienten (d.h. die Rückkopplung) auf Null setzen, die Definition auf unsere ursprüngliche FIR-Filterdefinition reduziert wird, was bedeutet, dass die FIR-Berechnung nur auf vergangenen und aktuellen Eingabewerten basiert, nämlich:
y(n)=\sum_{k=0}^{q}b_kx(n-k)
\)
Implementierung
Obwohl es mehrere praktische Implementierungen für FIRs gibt, sind die direkte Formularstruktur und ihr transponierter Vetter vielleicht die am häufigsten verwendete, und als solche sind alle entworfenen Filterkoeffizienten für die Implementierung in einer direkten Formularstruktur vorgesehen.
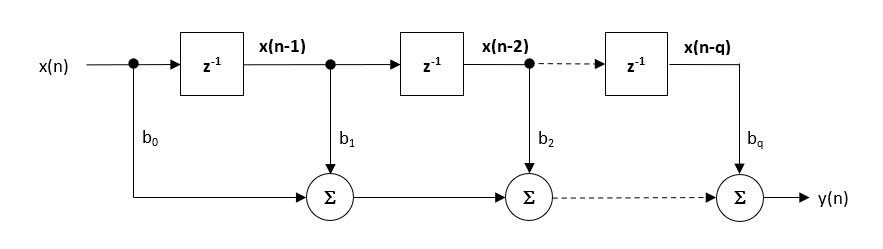
Die Struktur der Direktform und die zugehörige Differenzgleichung sind unten dargestellt. Die Direkte Form wird aufgrund des Einzelakkumulatorkonzepts für die Festkomma-Implementierung befürwortet.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)
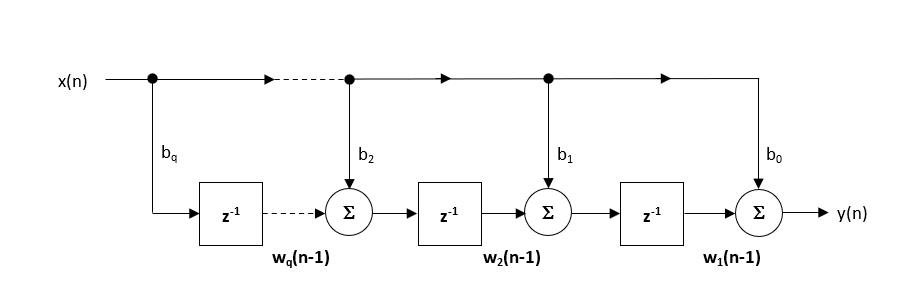
Die empfohlene (Standard-)Struktur innerhalb des ASN-Filter-Designers ist die direkte formtransponierte Struktur, da diese bei Verwendung der Fließkomma-Arithmetik eine höhere numerische Genauigkeit bietet. Dies ist leicht zu erkennen, wenn man die untenstehenden (für die Implementierung verwendeten) Differenzengleichungen analysiert, da die unerwünschten Auswirkungen der numerischen Überfüllung minimiert werden, da die Fließkomma-Addition bei Zahlen ähnlicher Größe durchgeführt wird.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)
Was haben wir gelernt?
Digitale Filter werden in die folgenden zwei Kategorien unterteilt:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
IIR-Filter (unendliche Impulsantwort) werden im Allgemeinen für Anwendungen gewählt, bei denen die lineare Phase nicht allzu wichtig ist und der Speicher begrenzt ist. Sie wurden in großem Umfang in der Audioentzerrung, der biomedizinischen Sensorsignalverarbeitung, intelligenten IoT/IIoT-Sensoren und Hochgeschwindigkeits-Telekommunikations-/RF-Anwendungen eingesetzt.
FIR-Filter (FIR = Finite Impuls Response) werden im Allgemeinen für Anwendungen gewählt, bei denen eine lineare Phase wichtig ist und eine angemessene Menge an Speicher und Rechenleistung zur Verfügung steht. Sie haben eine weite Verbreitung in Audio- und biomedizinischen Signalverbesserungsanwendungen.
ASN Filter Designer bietet Ingenieuren alles um komplexe digitale IIR- und FIR-Filter für eine Vielzahl von Sensoren für Messanwendungen zu entwerfen, zu experimentieren und einzusetzen. Diese Vorteile in Verbindung mit einer automatischen Dokumentations- und Codegenerierungsfunktionalität ermöglichen es Ingenieuren, einen IIR/FIR-Digitalfilter innerhalb von Minuten statt Stunden zu entwerfen und zu validieren.

