Verschil tussen IIR en FIR filters: een praktische ontwerp gids
Een digitaal filter is een wiskundig algoritme dat werkt op een digitale dataset (bijv. sensorgegevens) om informatie die van belang is te extraheren en ongewenste informatie te verwijderen. Toepassingen van dit soort technologie zijn onder andere het verwijderen van fouten in de sensorgegevens en het verwijderen van ruis op een gemeten signaal om de analyse van de gegevens te vergemakkelijken. Maar hoe kiezen we het beste type digitaal filter voor onze toepassing? En wat zijn de verschillen tussen een IIR-filter en een FIR-filter?
Er zijn 2 soort en digitale filters:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
Zoals de namen aangeven, wordt elk type filter gecategoriseerd op basis van de lengte van de impulsrespons. Alvorens te beginnen met een gedetailleerde wiskundige analyse is het echter verstandig om de verschillen in prestaties en kenmerken van elk type filter aan te geven.
Voorbeeld
Om de verschillen tussen een IIR en FIR te illustreren, is hieronder de frequentierespons van een 14e orde FIR (vaste lijn), en een 4e orde Chebyshev Type I IIR (stippellijn) in figuur 1 weergegeven. Merk op dat hoewel de magnitudespectra een vergelijkbare mate van verzwakking hebben, het fasespectrum van het IIR-filter niet-lineair is in de passband (\(\small 0\rightarrow7.5Hz\))), en zeer niet-lineair wordt bij de afsnijfrequentie, \(\small f_c=7.5Hz\). Merk ook op dat de FIR een hoger aantal coëfficiënten (15 vs de IIR’s 10) nodig heeft om de dempingskarakteristieken van het IIR aan te passen.
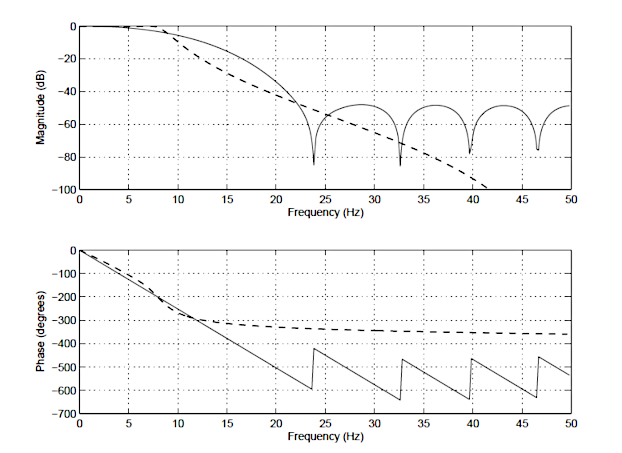
Dit zijn slechts enkele van de verschillen tussen de twee soorten filters. Een gedetailleerde samenvatting van de belangrijkste voor- en nadelen van elk type filter volgt nu.
IIR filters
IIR (infinite impulse response) filters worden over het algemeen gekozen voor toepassingen waarbij de lineaire fase niet al te belangrijk is en het geheugen beperkt is. Ze zijn op grote schaal toegepast in audio equalisatie, biomedische sensor signaalverwerking, IoT/IIoT smart sensors en hogesnelheids telecommunicatie/RF-toepassingen.
Voordelen
- Lage implementatiekosten: vereist minder coëfficiënten en geheugen dan FIR-filters om te voldoen aan een vergelijkbare set specificaties, d.w.z. afsluitingsfrequentie en stopbandverzwakking
- Lage latentie: geschikt voor real-time controle en zeer snelle RF-toepassingen door het lage aantal coëfficiënten
- Analoog equivalent: Kan worden gebruikt voor het nabootsen van de kenmerken van analoge filters met behulp van s-z plane mapping transformaties
Nadelen
- Niet-lineaire fasekarakteristieken: De fasekarakteristieken van een IIR-filter zijn over het algemeen niet-lineair, vooral in de buurt van de afsnijfrequenties. All-pass equalisation filters filters kunnen worden gebruikt om de passband fase karakteristieken te verbeteren
- Meer gedetailleerde analyse: Vereist meer schaling en numerieke overloopanalyse wanneer deze in een vast punt is geïmplementeerd. De Direct Form II filterstructuur is bijzonder gevoelig voor de effecten van kwantisering en vereist speciale zorg tijdens de ontwerpfase
- Numerieke stabiliteit: Minder numeriek stabiel dan hun FIR (finite impulse response) tegenhangers, vanwege de feedbackpaden
FIR filters
FIR (finite impulse response) filters worden over het algemeen gekozen voor toepassingen waar lineaire fase belangrijk is en waar een behoorlijke hoeveelheid geheugen en rekenkracht beschikbaar is. Ze worden op grote schaal toegepast in audio- en biomedische signaalverbeteringstoepassingen. Hun all-zero structuur (hieronder besproken) zorgt ervoor dat ze nooit onstabiel worden voor elk type ingangssignaal, wat ze een duidelijk voordeel geeft ten opzichte van de IIR.
Voordelen
- Lineaire fase: FIRs kunnen eenvoudig worden ontworpen om lineaire fase te hebben. Dit betekent dat er geen fasevervorming in het te filteren signaal wordt geïntroduceerd, aangezien alle frequenties in de tijd evenveel worden verschoven – waardoor hun relatieve harmonische relaties (d.w.z. constante groep en faseverschuiving) behouden blijven. Dit is zeker niet het geval bij IIR-filters, die een niet-lineaire fasekarakteristiek hebben
- Stabiliteit: Omdat FIR’s geen eerdere uitgangswaarden gebruiken om hun huidige uitgang te berekenen, d.w.z. ze hebben geen terugkoppeling, kunnen ze nooit instabiel worden voor enig soort ingangssignaal, wat ze een duidelijk voordeel geeft ten opzichte van IIR-filters
- Willekeurige frequentierespons: De Parks-McClellan en ASN FilterScript’s firarb() functie maken het mogelijk om een FIR te ontwerpen met een arbitraire magnituderespons. Dit betekent dat een FIR gemakkelijker kan worden aangepast dan een IIR
- Fixed point performance: de effecten van kwantificering zijn minder ernstig dan die van een IIR
Nadelen
- Hoge reken- en geheugenbehoefte: FIRs hebben meestal veel meer coëfficiënten nodig voor het bereiken van een scherpe cut-off dan hun IIR tegenhangers. Het gevolg hiervan is dat ze veel meer geheugen nodig hebben en aanzienlijk meer MAC-bewerkingen (meervoudige en geaccumuleerde). De moderne microcontrollerarchitecturen op basis van de Cortex-M-kernen van de arm bevatten nu echter DSP-hardwareondersteuning via SIMD (signaalinstructie, meerdere data) die de filtering aanzienlijk versnellen
- Hogere latentie: het hogere aantal coëfficiënten betekent dat een FIR over het algemeen minder geschikt is dan een IIR voor snelle high throughput toepassingen. Dit wordt problematisch voor real-time closed-loop control toepassingen, waarbij een FIR filter te veel groepsvertraging kan hebben om lusstabiliteit te bereiken
- Geen analoog equivalent: met behulp van de Bilinear, matched z-transform (s-z mapping) kan een analoog filter eenvoudig worden omgezet in een gelijkwaardig IIR filter. Dit is echter niet mogelijk voor een FIR omdat deze geen analoog equivalent heeft
Wiskundige definities
Zoals besproken in de inleiding, zijn de namen IIR en FIR afkomstig van de wiskundige definities van elk type filter, d.w.z. een IIR-filter wordt gecategoriseerd op basis van zijn theoretisch oneindige impulsrespons
y(n)=\sum_{k=0}^{\infty}h(k)x(n-k)
\)
en een FIR gecategoriseerd door zijn eindige impulsrespons,
y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)
\)
We zullen nu de wiskundige eigenschappen van elk type filter op zijn beurt analyseren.
IIR definitie
Zoals hierboven gezien, wordt een IIR-filter gecategoriseerd door zijn theoretisch oneindige impulsrespons,
\(\displaystyle y(n)=\sum_{k=0}^{\infty}h(k)x(n-k) \)Praktisch gezien is het niet mogelijk om de output van een IIR te berekenen met deze vergelijking. Daarom kan de vergelijking worden herschreven in termen van een eindig aantal polen \(\small p\) en nullen \(\small q\)zoals gedefinieerd door de lineaire constante coëfficiënt verschilvergelijking gegeven door:
waarbij \(\small a_k\) en \(\small b_k\) de noemer en de teller van de polynomiale coëfficiënten van het filter zijn, waarvan de wortels gelijk zijn aan respectievelijk de polen en nullen van het filter. Zo kan een relatie tussen de verschilvergelijking en de z-transformatie (overdrachtsfunctie) worden gedefinieerd door gebruik te maken van de z-transformatievertragingseigenschap, zodat,
\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)\quad\stackrel{\displaystyle\mathcal{Z}}{\longleftrightarrow}\quad\frac{\sum\limits_{k=0}^q b_kz^{-k}}{1+\sum\limits_{k=1}^p a_kz^{-k}}
\)
Zoals gezien is de overdrachtsfunctie een frequentiedomein representatie van het filter. Merk ook op dat de polen werken op de uitvoergegevens, en de nullen op de invoergegevens. Aangezien de polen op de uitgangsdata werken en de stabiliteit beïnvloeden, is het essentieel dat hun stralen binnen de eenheidscirkel (d.w.z. <1) blijven voor BIBO-stabiliteit (bounded input, bounded output). De stralen van de nullen zijn minder kritisch, omdat ze de stabiliteit van het filter niet beïnvloeden. Dit is de belangrijkste reden waarom all-zero FIR (finite impulse response) filters altijd stabiel zijn.
y(n)=\sum_{k=0}^{q}b_k x(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
BIBO-stabiliteit
Een lineair tijdsinvariant (LTI) systeem (zoals een digitaal filter) is naar verluidt een gebonden ingang, gebonden uitgang stabiel, of BIBO stabiel, als elke gebonden ingang aanleiding geeft tot een gebonden uitgang, zoals
Waar \(\small h(k)\) de impulsrespons van het LTI-systeem is. Bij het analyseren van deze vergelijking moet duidelijk zijn dat aan het BIBO-stabiliteitscriterium alleen wordt voldaan als de polen van het systeem binnen de eenheidscirkel liggen, aangezien het ROC (gebied van convergentie) van het systeem de eenheidscirkel moet omvatten. Het is dus voldoende om te zeggen dat een begrensd ingangssignaal altijd een begrensd uitgangssignaal zal produceren als alle polen binnen de eenheidscirkel liggen.
De nullen daarentegen worden niet beperkt door deze eis en kunnen dus overal op het z-vlak liggen, omdat ze niet direct van invloed zijn op de stabiliteit van het systeem. Daarom kan een systeemstabiliteitsanalyse worden uitgevoerd door eerst de wortels van de overdrachtsfunctie (d.w.z. de wortels van de teller- en noemerpolynomialen) te berekenen en dan de corresponderende polen en nullen op het z-vlak te plotten.
Een interessante situatie ontstaat als er polen op de eenheidscirkel liggen, omdat het systeem naar verluidt marginaal stabiel is, omdat het noch stabiel, noch instabiel is. Hoewel marginaal stabiele systemen niet BIBO stabiel zijn, zijn ze door digitale oscillatorontwerpers uitgebuit, omdat hun impulsrespons een eenvoudige methode biedt om sinusgolven te genereren, die van onschatbare waarde zijn gebleken op het gebied van telecommunicatie.
Biquad IIR filters
De hierin besproken IIR-filterimplementatie zou biquad zijn, aangezien deze twee polen en twee nullen heeft, zoals hieronder in figuur 2 wordt geïllustreerd. De biquad-implementatie is vooral nuttig voor vaste-punt-implementaties, aangezien de effecten van kwantisatie en numerieke stabiliteit tot een minimum worden beperkt. Het algemene succes van een biquadimplementatie is echter afhankelijk van de beschikbare nauwkeurigheid van de getallen, die voldoende moet zijn om ervoor te zorgen dat de gekwantificeerde polen altijd binnen de eenheidscirkel liggen.
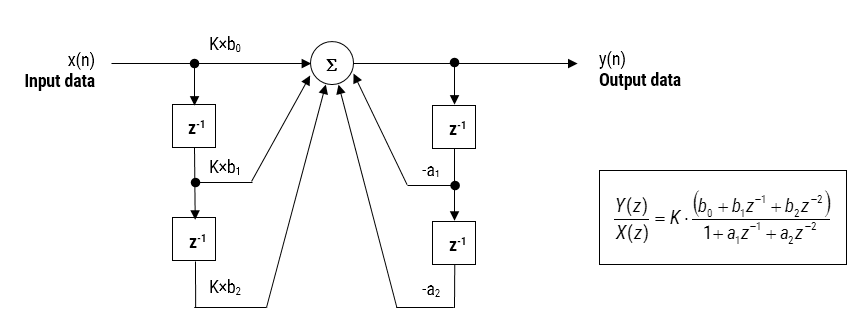
Figuur 2: Directe Form I (biquad) IIR filter realisatie en transfer functie
Bij het analyseren van figuur 2 is te zien dat de biquad structuur in feite bestaat uit twee feedbackpaden (geschaald met (scaled by \(\small a_1\) en \(\small a_2\))), drie feed forward paden (geschaald met \(\small b_0, b_1\) and \(\small b_2\)) en een sectieversterking, \(\small K\). Zo kan de filterwerking van figuur 1 worden samengevat met de volgende eenvoudige recursieve vergelijking:
\(\displaystyle y(n)=K\times\Big[b_0 x(n) + b_1 x(n-1) + b_2 x(n-2)\Big] – a_1 y(n-1)-a_2 y(n-2)\)Bij het analyseren van de vergelijking valt op dat de biquadimplementatie slechts vier toevoegingen vereist (waarvoor slechts één accumulator nodig is) en vijf vermenigvuldigingen, die gemakkelijk kunnen worden ondergebracht op elke Cortex-M microcontroller. De sectieaanwinst,\(\small K\) kan ook vooraf worden vermenigvuldigd met de voorwaartse padcoëfficienten vóór de implementatie.
Een verzameling van Biquad-filters wordt een Biquad-cascade genoemd, zoals hieronder geïllustreerd.

De ASN Filterontwerper kan een cascade van maximaal 50 biquads ontwerpen en uitvoeren (alleen in professionele uitvoering).
Floating point (Drijvend punt) implementatie implementation
Bij de toepassing van een filter in floating point (d.w.z. bij gebruik van dubbele of enkelvoudige precisieberekeningen) worden Direct Form II-structuren als een betere keuze beschouwd dan de Direct Form I-structuur. De Direct Form II getransponeerde structuur wordt beschouwd als de meest numeriek nauwkeurige voor de implementatie van zwevende punten, aangezien de ongewenste effecten van numerieke zweving tot een minimum worden beperkt, zoals blijkt uit de analyse van de differentiaalvergelijkingen.
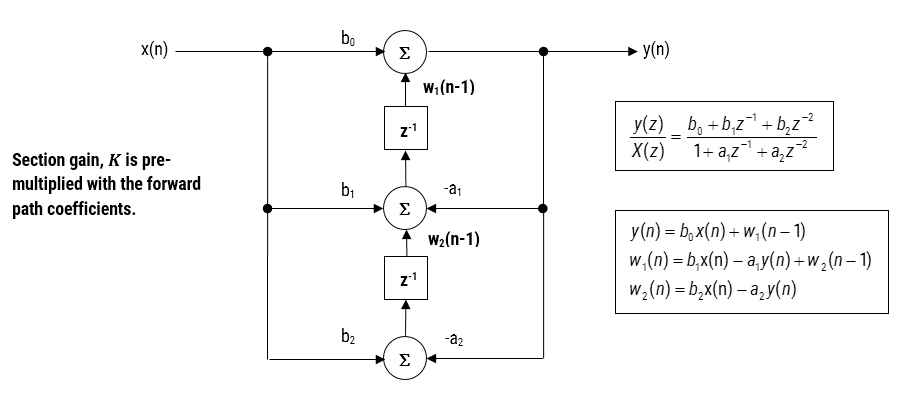
Figuur 3 – Directe vorm II omzetting van structuur, overdrachtsfunctie en verschilvergelijkingen
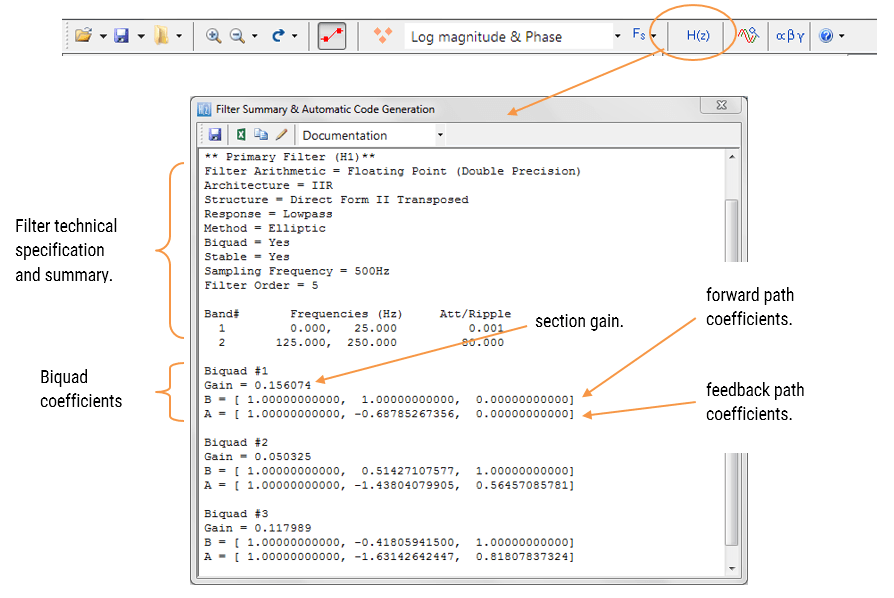
Het filteroverzicht (weergegeven in Figuur 4) geeft de ontwerper een gedetailleerd overzicht van het ontworpen filter, inclusief een gedetailleerd overzicht van de technische specificaties en de filtercoëfficiënten, dat een snelle en eenvoudige route biedt om uw ontwerp te documenteren.
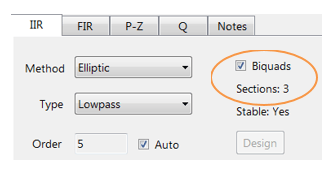
De ASN Filter Designer ondersteunt het ontwerp en de implementatie van zowel single section als Biquad (standaardinstelling) IIR filters.
FIR definitie
De vergelijking van het verschil in lineaire constante coëfficiënten van het IIR wordt weergegeven, d.w.z.
y(n)=\sum_{k=0}^{q}b_kx(n-k)-\sum_{k=1}^{p}a_ky(n-k)
\)
Merk op dat wanneer we de\(\small a_k\) coëfficiënten (d.w.z. de terugkoppeling) op nul zetten, de definitie herleidt tot onze oorspronkelijke FIR filterdefinitie, wat betekent dat de FIR-berekening gewoon gebaseerd is op vroegere en huidige invoerwaarden, namelijk:
y(n)=\sum_{k=0}^{q}b_kx(n-k)
\)
Implementatie
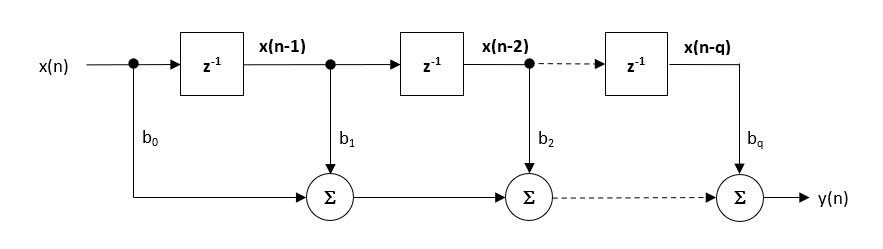
Hoewel er verschillende praktische implementaties voor FIR’s bestaan, zijn de directe vormstructuur en de getransponeerde neef misschien wel de meest gebruikte en als zodanig zijn alle ontworpen filtercoëfficiënten bedoeld voor implementatie in een directe vormstructuur.
De Direct Form-structuur en de bijbehorende verschilvergelijking worden hieronder weergegeven. De Direct Form wordt bepleit voor implementatie in een vaste vorm op basis van het concept van een enkele accumulator.
\(\displaystyle y(n) = b_0x(n) + b_1x(n-1) + b_2x(n-2) + …. +b_qx(n-q) \)
De aanbevolen (standaard) structuur binnen de ASN Filter Designer is de Direct Form Transposed structure, omdat deze een superieure numerieke nauwkeurigheid biedt bij het gebruik van floating point arithmetic. Dit is goed te zien aan de hand van de onderstaande verschilvergelijkingen (gebruikt voor de implementatie), aangezien de ongewenste effecten van numerieke swamping worden geminimaliseerd, aangezien de optelling van de drijvende komma wordt uitgevoerd op getallen van een vergelijkbare grootte.
\(\displaystyle \begin{eqnarray}y(n) & = &b_0x(n) &+& w_1(n-1) \\ w_1(n)&=&b_1x(n) &+& w_2(n-1) \\ w_2(n)&=&b_2x(n) &+& w_3(n-1) \\ \vdots\quad &=& \quad\vdots &+&\quad\vdots \\ w_q(n)&=&b_qx(n) \end{eqnarray}\)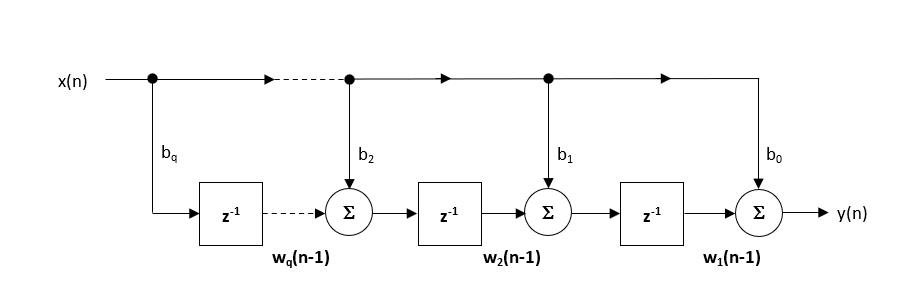
Wat hebben we geleerd?
Digitale filters zijn onderverdeeld in de volgende twee categorieën:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
IIR (infinite impulse response) filters worden over het algemeen gekozen voor toepassingen waarbij de lineaire fase niet al te belangrijk is en het geheugen beperkt is. Ze zijn op grote schaal toegepast in audioverevening, biomedische sensorsignaalverwerking, IoT/IIoT smart sensors en hogesnelheidstelecommunicatie/RF-toepassingen.
FIR (finite impulse response) filters worden over het algemeen gekozen voor toepassingen waar lineaire fase belangrijk is en een behoorlijke hoeveelheid geheugen en rekenkracht beschikbaar is. Ze worden op grote schaal toegepast in audio- en biomedische signaalverbeteringstoepassingen.
ASN Filter Designer biedt ingenieurs alles wat ze nodig hebben om complexe IIR en FIR digitale filters te ontwerpen, te experimenteren en in te zetten voor een verscheidenheid aan sensor meetapplicaties. Deze voordelen in combinatie met automatische documentatie en codegeneratiefunctionaliteit stellen ingenieurs in staat om een IIR/FIR digitaal filter te ontwerpen en te valideren binnen enkele minuten in plaats van uren.
